Рекомендації по організації самостійної роботи

Кафедра вищої математики ДУТ пропонує кожному студенту врахувати наступні рекомендації:

1. Враховуючи свої індивідуальні особливості та можливості, обчислити реальний час для самостійної роботи у семестрі та частину цього часу на вивчення вищої математики. Для якісного засвоєння навчальної програми семестру з вищої математики студенту-заочнику потрібно біля 150 академічних годин.

2. Придбати загальний зошит на 48-96 сторінок і оформити його титульний лист так:

Робочий зошит

з вищої математики на 6 семестр

студента (ки) 3 курсу, групи ________,

факультету _______________________

_________________________________

^{(прізвище ім’я, по-батькові)}

залікова книжка № __________

Зошит

початий ______ закінчений ________

перевірений викладачем _______ _________________

^{(підпис) (прізвище та ініціали)}

Дата _______

3. Для вивчення матеріалу певного розділу студенту потрібно:

а) уважно прочитати рекомендовані сторінки, ознайомитись із змістом екзаменаційних завдань відповідного розділу, щоб визначити основу цього розділу та його типові приклади;

б) в робочому зошиті записати стислі відповіді на усі завдання розділу, який вивчається, з обов’язковим розв’язуванням заданих прикладів ( – номер варіанту, що визначається за останньою цифрою номера залікової книжки: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10). Завдання типу 1.1, 1.2, … 1.10 виконується одне кожним студентом в залежності від останньої цифри залікової книжки.

4. Коли виникають складності у відповідях на теоретичні завдання або при розв’язуванні прикладів, треба відповідний матеріал знову знайти у підручнику (або в додатковій літературі), ознайомитись повторно, більш уважно і, при необхідності, з викладачем на консультації.

Зауваження 1. Для виконання третьої рекомендації студенту потрібно 7-10 астрономічних годин. Доцільно цю роботу виконати в один день.

Зауваження 2. Кожному студенту буде дозволено під час семестрового заліку користуватись лише своїм власноруч написаним робочим зошитом.

Питання навчальної програми та задачі для підготовки до екзамену з дисципліни вища математика

Дискретна математика.

Завдання № 1. Спростити вирази алгебри множин:

№ варіанта	Вираз
1
2
3
4
5
6
7
8
9
10

Завдання № 2. Розв’язати задачу з комбінаторики:

3.1. 1) У музичному гуртку навчаються 10 чоловік, у гуртку художнього слова – 15, у вокальному гуртку – 12, в фотогуртку – 20. Скількома способами можна утворити бригаду із чотирьох читців, трьох музикантів, п’яти співаків і одного фотографа?

2) Скільки чотиризначних чисел, які містять цифру 3, можна утворити з цифр 0,1,2,3,4,5 , якщо в кожному числі жодна з цифр не повторюється?

3.2. Скількома способами 5 юнаків можуть запросити в кіно 5 з 7 дівчат?

2) Із групи в 15 чоловік треба виділити бригадира і 4 члена бригади. Скількома способами це можна зробити?

3.3. 1) П’ять учнів треба розподілити у п’ять паралельних класів. Скількома способами це можна зробити?

2) Скільки тризначних чисел, що діляться на 3, можна утворити з цифр 0,1,2,3,4,5 , якщо в кожному числі жодна з цифр не повторюється?

3.4. 1) Ліфт зупиняється на десяти поверхах. Скількома способами можуть вийти 8 пасажирів, що знаходяться в кабіні ліфта?

2) Скількома способами можна розподілити 28 кісток доміно міх чотирма гравцями?

3.5. 1) Скільки різних десятизначних чисел можна написати, використовуючи тільки цифри 1 і 2?

2) У шаховому турнірі беруть участь 8 шахістів третього розряду, 6 – другого і 2 першорозрядники. Визначити кількість таких складів учасників першого туру, щоб шахісти однієї категорії зустрічалися між собою.

3.6. 1) Скільки різних двозначних чисел можна утворити з цифр 1,2,3,4 за умови, що в кожному числі немає однакових цифр?

2) Сім яблук і три апельсини треба покласти в два пакети так, щоб у кожному пакеті був хоча б один апельсин і щоб кількість фруктів у них була однаковою. Скількома способами це можна зробити?

3.7. 1) З цифр 0,1,2,3 складені різні чотиризначні числа так, що у кожному числі немає однакових цифр. Скільки таких чисел? Скільки серед них парних чисел 2) Знаки азбуки Морзе складаються із символів „ ” і „ - ”. Скільки слів можна зобразити за умови, що кожне слово містить не більше п’яти символів?

3.8. 1) Скільки існує шестизначних чисел, усі цифри яких непарні?

2) Вісім авторів повинні написати книгу з шістнадцяти глав. Скількома способами можна розподілити матеріал між авторами, якщо два автори напишуть по три глави, чотири – по дві і два – по одній главі книги?

3.9. 1) Скільки різних натуральних чисел можна скласти з цифр 0,1,2,3,4. якщо в кожне число кожна дана цифра входить не більше одного разу?

2) Садівник повинен протягом трьох днів посадити 10 дерев. Скількома способами він може розподілити за днями свою роботу, якщо буде висаджувати не менше одного дерева в день?

3.10. 1) Скільки різних двозначних чисел можна скласти з цифр 0,1,2,3, якщо всі цифри 0,1,2 входять у кожне число не більше одного разу?

2) Із вази, де стоять 10 червоних і 4 рожевих гвоздики, вибирають одну червону і дві рожеві квітки. Скількома способами це можна зробити?

Завдання № 3. Для булевої функції , заданої формулою:

1) скласти таблицю істинності;

2) знайти ДДНФ і ДКНФ двома способами:

а) за допомогою таблиці,

б) за допомогою рівносильних перетворень.

3) знайти представлення у вигляді многочлена Жегалкіна.

№ варіанта	Булева функція
1
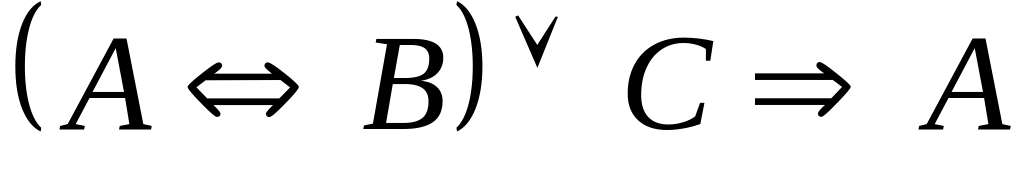
2
3
4
5
6
7
8
9
10

Завдання № 4. Орграф заданий матрицею суміжності , яка подана у блочному вигляді. Треба:

1. намалювати орграф;

2. знайти всі шляхи довжини 2 і 3;

3. знайти степені вершин , , , ;

4. знайти компоненти зв’язності та сильної зв’язності;

5. побудувати граф конденсації 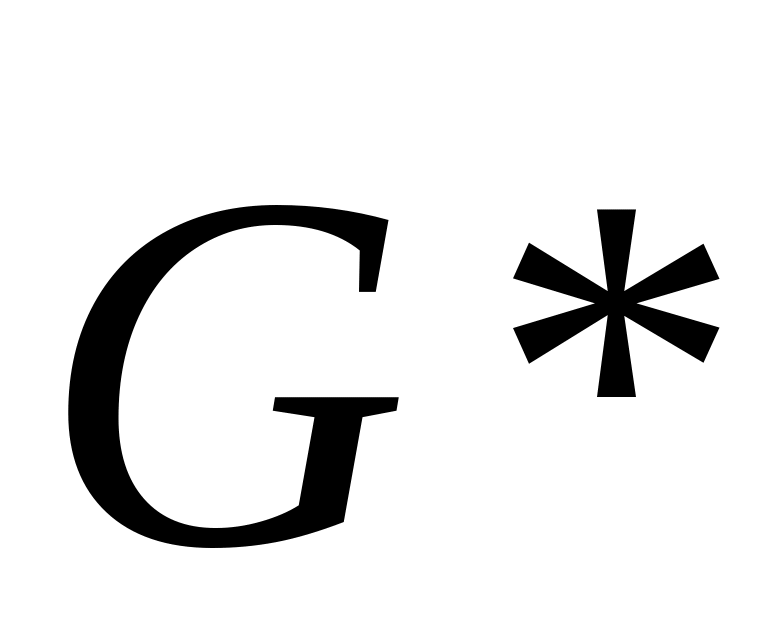графа ;

6. визначити тип зв’язності графа ;

7. знайти матрицю інцидентності ;

1. ; 4. ; 7. ;

2. ; 5. ; 8. ;

3. ; 6. ; 9. ; 10.

Блоки матриці суміжності:

; ;

; ;

; ;

; .