Получили, что , двигаясь из положения 1 в положение 2
по разным траектории 1а2 и |
|
1б2, точка совершает |
одно и то же перемещение |
r |
, |
следовательно, работы одинаковы:
А1a2 = А1b2.
Таким образом, сила тяжести – консервативная сила.
Консервативной является также сила упругости.
Неконсервативные силы
Неконсервативной называется сила, работа которой зависит от формы пути, по которому материальная точка переходит из начального положения в конечное.
Вмеханике неконсервативной силой будет являться сила трения.
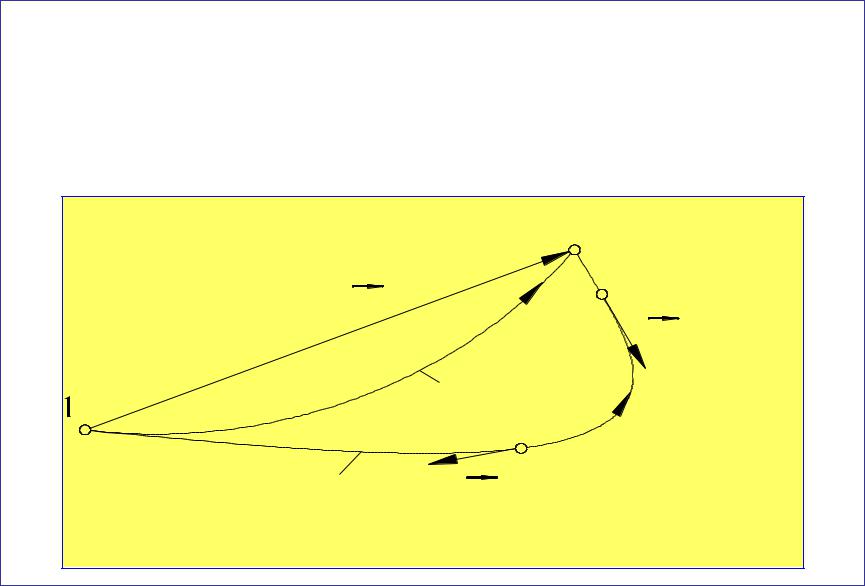
Найдем работу силы трения, действующей на тело при |
||
перемещении его из точки 1 в точку 2 по |
||
горизонтальной поверхности по двум разным путям |
||
S1a2 и S1b2 . |
|
|
|
|
2 |
r |
|
a |
|
Fòð |
|
|
|
|
|
S1a2 |
тр |
|
b |
|
S1b2 |
òð |
|
|
Fтр |
|
Искомые значения работ соответственно равны:
2 |
|
|
|
2 |
|
|
A1a2 (Fтр dr) |
|
A1b2 (Fтр dr) |
||||
1 |
|
|
|
1 |
|
|
(a) |
|
|
|
(b) |
|
|
|
|
|
|
|
|
|
Направление силы трения в процессе перемещения тела изменяется, поэтому Fтр выносить за знак интеграла нельзя.
|
|
2 |
r |
|
a |
|
Fòð |
|
|
S1a2 |
|
|
b |
|
S1b2 |
Fòð |
|
Так как F |
в любой точке траектории направлена |
|||
тр |
|
|
, то проекция F |
на dr |
противоположно |
dr |
|||
|
|
тр |
|
|
одна и та же во всех точках траектории и её можно вынести за знак интеграла.
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
А1a2 Fтр |
|
dr |
|
cos π Fтр dr |
|
|
|||||
|
|
|
|
|
|||||||
1 |
|
|
|
|
|
1 |
|
||||
a |
|
|
|
|
|
a |
|||||
2 |
|
|
|
|
|
|
|
|
|
|
|
Fтр dS Fтр S1a2 |
|
|
|
|
|
|
|||||
1 |
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
А1бб Fтр |
|
dr |
|
cos π Fтр dr |
|
|
|||||
|
|
|
|
|
|||||||
1 |
|
|
|
|
|
1 |
|
||||
б |
|
|
|
|
б |
||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
Fтр dS Fтр S1бб |
|
|
|
|
|
|
|||||
1 |
|
|
|
|
|
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
Так как |
|
, то и |
|
S1a 2 S1б2 |
A1a 2 A1б2 |
||
|
|
|
|
Таким образом, сила трения скольжения - неконсервативная сила
Силовое поле, в котором действуют консервативные силы, называется потенциальным.
К потенциальным полям относится гравитационное и электростатическое поле.
Силовое поле, в котором действуют неконсервативные силы, называется вихревым.
К вихревым полям относится магнитное поле.
Вэтом поле действуют неконсервативные сила Ампера
иЛоренца.
4.3. Полная механическая энергия
Способность различных форм движения к взаимным превращениям привели к мысли о том, что должна существовать единая мера различных форм движения.
Эта мера характеризует любое движение с точки зрения возможностей превращения его в другие формы.
Полная механическая энергия – единая мера различных форм движения материи и типов взаимодействия материальных объектов.
Полная механическая энергия является однозначной, непрерывной, конечной, дифференцируемой функцией состояния объекта.
Функция состояния – такая физическая характеристика объекта, изменение которой при переходе объекта из одного состояния в другое не зависит от пути перехода и целиком определяется параметрами начального и конечного состояний.
Материальные объекты:
-могут участвовать в разных взаимодействиях;
-могут участвовать в различных формах движения;
-могут перемещаться в пространстве;
-в них могут происходить различные процессы (молекулярные, электромагнитные, ядерные и др.).
Обычно изменения, обусловленные участием объекта в различных типах взаимодействий и формах движения, рассматривают отдельно.
Всвязи с этим энергию определяют как сумму нескольких слагаемых, каждое из которых зависит только от одного или двух параметров.