2.11. Электромагнитная индукция. Основной закон электромагнитной индукции

Закон электромагнитной индукции(закон Фарадея – Максвелла)

ЭДС электромагнитной индукции в контуре численно равна скорости изменения магнитного потока сквозь поверхность, натянутую на этот контур, т. е.

.

Закон электромагнитной индукции можно также записать в форме

,

где _потокосцепление электрической цепи.

Знак «минус» в выражении для ЭДС индукции объясняется правилом Ленца

«При всяком изменении магнитного потока сквозь поверхность, натянутую на замкнутый проводящий контур, в контуре возникает индукционный ток такого направления, что его собственное магнитное поле противодействует изменению магнитного потока, вызвавшему индукционный ток» (рис. 2.18).

Явление электромагнитной индукции в неподвижном замкнутом проводнике объясняется тем, что переменное магнитное поле вызывает появление вихревого электрического поля, циркуляция напряжённости которого вдоль замкнутого проводящего контураLравна ЭДС электромагнитной индукции

_вихр.d=.

Явление электромагнитной индукции в проводнике, движущемся в постоянном магнитном поле, объясняется действием силы Лоренца: разделение зарядов в проводнике (т.е. создание ЭДС) производится составляющей силы Лоренца, параллельной проводнику; составляющая, перпендикулярная проводнику, тормозит его движение (поэтому необходимо прикладывать внешнюю силу для создания ЭДС). Работа силы Лоренца в целом равна нулю.

2.12. Явление самоиндукции

Самоиндукцией называется возникновение ЭДС электромагнитной индукции в электрической цепи вследствие изменения потокосцепления самоиндукции и находится по формуле

,

где _S– потокосцепление самоиндукции рассматриваемого контура.

Индуктивностьюконтура называется положительная скалярная величина, численно равная потокосцеплению самоиндукции контура при силе тока в контуре 1 А.

Индуктивность зависит от размеров и формы контура, от магнитной проницаемости среды и в отсутствие ферромагнетиков не зависит от силы тока в контуре.

L = _S / I.

Индуктивность длинного соленоида

L = _^S / l = _n²V,

где относительная магнитная проницаемость среды, заполняющей весь объём соленоида ,V = lS;l длина соленоида,Sплощадь одного витка,Nобщее число витков,nчисло витков, приходящихся на единицу длины соленоида.

ЭДС самоиндукции

.

Если контур не деформируется и находится в неферромагнитной среде, то

.

Электродвижущая сила самоиндукции противодействует, в соответствии с правилом Ленца, изменению тока в цепи, замедляя его убывание или возрастание.

При замыкании цепи начальный ток I₀=0 и зависимость силы тока от времени имеет вид

.

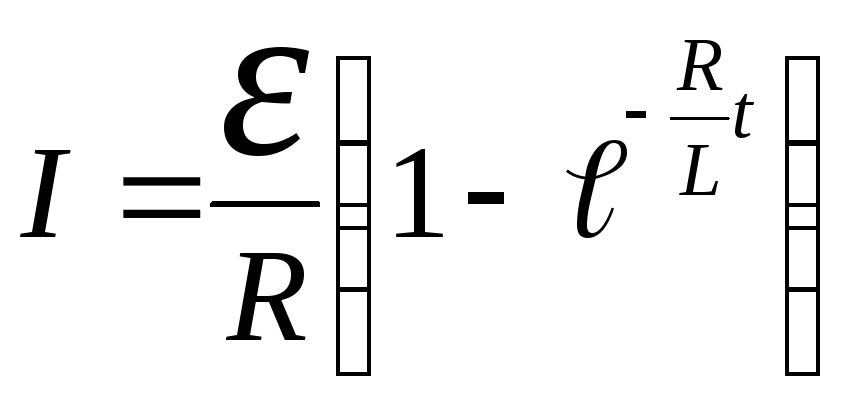При отключении источника ЭДС (без изменения сопротивления Rцепи) ток в цепи спадает по закону

,

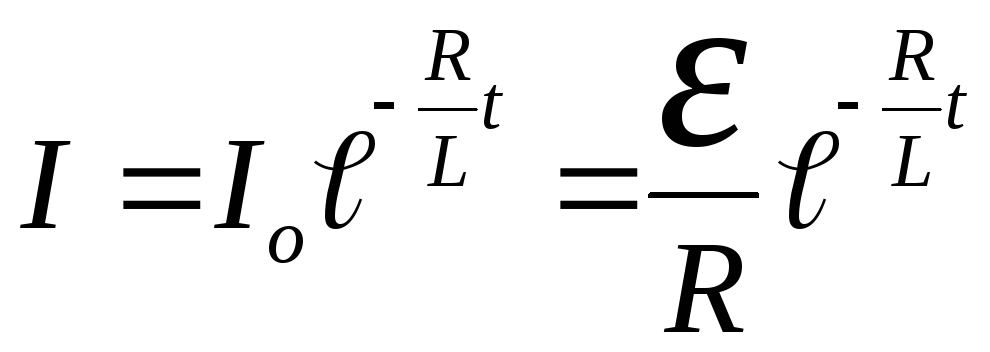где Rэквивалентное сопротивление цепи, включенное последовательно с индуктивностью;Lиндуктивность цепи; ЭДС источника, действующего в цепи.

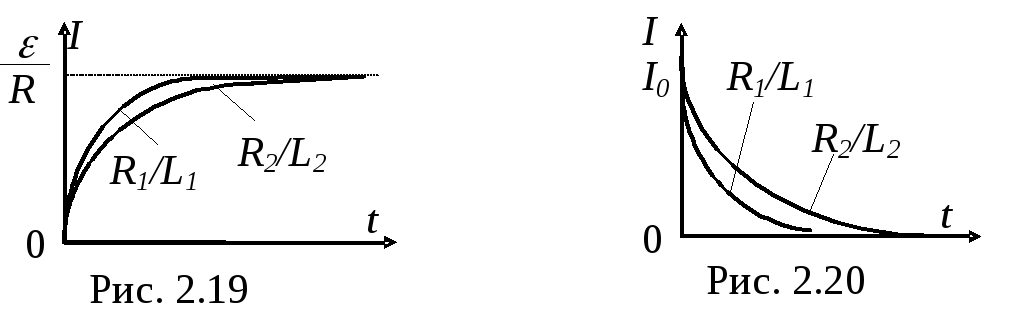
Графики зависимости силы тока от времени приведены на рис. 2.19 и 2.20.

2.13. Взаимная электромагнитная индукция

Взаимной индукцией называется явление возникновения ЭДС электромагнитной индукции в одной электрической цепи при изменении электрического тока в другой цепи или при изменении взаимного расположения этих двух цепей.

ЭДС взаимной индукции, возникающая во второй цепи вследствие изменения потокосцепления ₂₁взаимной индукции этой цепи и другой (первой) цепи с током, рассчитывается по формуле

.

Потокосцепление ₂₁обусловлено магнитным полем токаI₁в первой цепи и, при прочих равных условиях, пропорционально силе тока I₁

_L₂₁I₁,

где L₂₁взаимная индуктивность второго и первого контуров (цепей). В отсутствие ферромагнетиков она зависит от размеров и формы контуров, их взаимного расположения, магнитной проницаемости среды и не зависит от силы тока. Если контуры находятся в неферромагнитной среде, тоL₁₂ = L₂₁. ЕслиL₁₂=L₂₁=const, то ЭДС взаимной индукции

и .