Лекция 20

План лекции:

• Стационарное уравнение Шредингера для атома водорода (в сферических координатах) Собственные волновые функции и квантовые числа, характеризующие состояние электрона в атоме.

• Собственная волновая функция, описывающая основное состояние атома водорода.

• Радиальное распределение плотности вероятности обнаружения электрона.

• Квантовый гармонический и ангармонический осцилляторы.

• Молекулярные спектры.

Стационарное уравнение Шредингера для атома водорода (в сферических координатах). Собственные волновые функции и квантовые числа, характеризующие состояние электрона в атоме.

Для того чтобы дать определение стационарному уравнению Шредингера для атома водорода (в сферических координатах), сначала следует рассказать о частице в одномерной прямоугольной “потенциальной яме” с бесконечно высокими стенками.

Так что же, сперва рассмотрим одномерную “потенциальную яму”:

Рис. 20.1 (Потенциальная яма)

Где - ширина “ямы”, а энергия отсчитывается от ее дна

Уравнение Шредингера для стационарных состояний в пределах ямы:

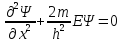(20.1)

Или

+(20.2)

(20.3)

За пределы “ямы” частица не проникает, поэтому волновая функция вне “ямы” равна нулю, следовательно, на границах “ямы” непрерывная волновая функция также должна обращаться в нуль:

(20.4)

Этим граничным условиям удовлетворяет решение уравнения Шредингера

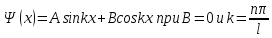(20.5)

Поскольку ,

то

(20.6)

(n=1,2,3,….) –собственные значения энергии.

При этом минимально возможное значение энергии

(20.7)

Таким образом, энергия частицы в бесконечно высокой потенциальной “яме” принимает лишь определенные дискретные значения, т. е. квантуется.

Квантовые значения энергии называются уровнями энергии, а число n, определяющее энергетические уровни частицы называется главным квантовым числом.

Собственные волновые функции , с учетом нормировки

xdx=1 (20.8)

будут иметь вид:

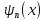= (20.9)

Рис. 20.2

На рисунке (Рис. 20.2) изображены графики собственных функция (а) и плотность вероятности (б) обнаружения частицы на разных расстояниях от “стенок” ямы, определяемая выражением.

=

Туннельный эффект.

Рис.20.3

Рассмотрим простейший потенциальный барьер прямоугольной формы (высота U и ширина l) для одномерного движения частицы (Рис. 20.3)

Вид волновых функция, являющихся решениями уравнения Шредингера для областей 1, 2 и 3 (см. рисунок 20.3 и таблицу 20.1) свидетельствует о том, что:

• В области 1 волновая функция представляет собой сумму двух плоских волн- движущейся в сторону барьера и отраженной от барьера.

• В области 2 в случае E>U

q=i, где β=

• В области 3 имеется только волна, прошедшая через барьер (=0), которая имеет вид волн де Бройля с той же длиной волны, но меньшей амплитудой.

Область	Уравнение Шредингера	Общее решение	Решение при E<U
1	+
2	+
3	+		(x)=

Таблица 20.1

Здесь

,

Таким образом, квантовая механика приводит к принципиально новому специфическому квантовому явлению, получившему название туннельного эффекта, в результате которого микрообъект может “пройти” сквозь потенциальный барьер (Рис. 20.4)

Для описания туннельного эффекта используют понятие коэффициента прозрачности D потенциального барьера, определяемого как отношение квадратов модулей прошедшей и падающей волны. Для случая прямоугольного потенциального барьера

) (20.11)

Рис. 20.4

Для потенциального барьера произвольной формы

Прохождение частицы сквозь область, в которую, согласно законам классической механики, она не может проникнуть, можно пояснить соотношением неопределенностей. Неопределенность импульса на отрезке составляет Связанная с этим разбросом в значениях импульса кинетическая энергия может оказаться достаточной для того, чтобы полная энергия частицы оказалась больше потенциальной.

Стационарное уравнение Шредингера для атома водорода (в сферических координатах)

Решение уравнения Шрёдингера для водородного атома использует факт, что кулоновский потенциал является изотропным, то есть не зависит от направления в пространстве, другими словами, обладает сферической симметрией. Хотя конечные волновые функции (орбитали) не обязательно сферически симметричны, их зависимость от угловой координаты следуют полностью из изотропии основного потенциала: собственные значения оператора Гамильтона можно выбрать в виде собственных состояний оператора углового момента. Это соответствует тому факту, что угловой момент сохраняется при орбитальном движении электрона вокруг ядра. Отсюда следует, что собственные состояния гамильтониана задаются двумя квантовыми числами углового момента l и m (целые числа). Квантовое число углового момента l может принимать значения 0, 1, 2… и определяет величину углового момента. Магнитное квантовое число может принимать m = −l, …, +l; оно определяет проекцию углового момента на (произвольно выбранную) ось z.

В дополнение к математическим выражениям для волновых функций полного углового момента и проекции углового момента, нужно найти выражение для радиальной зависимости волновой функции. В потенциале 1 радиальные волновые функции записываются с использованием полиномов Лагерра). Это приводит к третьему квантовому числу, которое называется основным квантовым числом n и может принимать значения 1, 2, 3… Основное квантовое число в атоме водорода связано с полной энергией атома. Заметим, что максимальное значение квантового числа углового момента ограничено основным квантовым числом: оно может изменяться только до n − 1, то есть l = 0, 1, …, n−1.

Из-за сохранения углового момента состояния с одинаковыми l, но различными m в отсутствие магнитного поля имеют одну и ту же энергию (это выполняется для всех задач с аксиальной симметрией). Кроме того, для водородного атома состояния с одинаковыми n, но разными l также вырождены (то есть имеют одинаковую энергию). Однако это свойство особенность лишь атома водорода (и водородоподобных атомов), оно не выполняется для более сложных атомов, которые имеют (эффективный) потенциал, отличающийся от кулоновского (из-за присутствия внутренних электронов, экранирующих потенциал ядра).

Если мы примем во внимание спин электрона, то появится последнее, четвёртое квантовое число, определяющее состояния атома водорода проекция углового момента собственного вращения электрона на ось Z. Эта проекция может принимать два значения. Любое собственное состояние электрона в водородном атоме полностью описывается четырьмя квантовыми числами. Согласно обычным правилам квантовой механики, фактическое состояние электрона может быть любой суперпозицией этих состояний. Это объясняет также, почему выбор оси Z для квантования направления вектора углового момента является несущественным: орбиталь для данных l и полученных для другой выделенной оси  всегда представляется как подходящая суперпозиция различных состояний с разными m (но тем же самым l), которые были получены для Z.

Рассмотрим сейчас решение уравнения Шрёдингера для атома водорода. Так как потенциальная функция электрона в атоме водорода имеет вид

(20.12)

 где e - заряд электрона (и протона), r радиус-вектор, то уравнение Шрёдингера запишется следующим образом:

(20. 13)

Здесь ψ — волновая функция электрона в системе отсчёта протона, m — масса электрона, — постоянная Планка, E — полная энергия электрона,

— оператор Лапласа. Так как потенциальная функция зависит от r, а не от координат по отдельности, удобно будет записать лапласиан в сферической системе координат  В ней он выглядит следующим образом:

(20.14)

Уравнение Шрёдингера в сферических координатах:

(20.15)

В этом уравнении   функция трёх переменных  Разделим его на три более простых уравнения. Для этого представим функцию   как произведение трех функций: Эти функции будем обозначать просто  Тогда:

(20.16)

После подстановки значений частных производных в уравнение Шрёдингера получим:

(20.17)

Умножим уравнение на 

(20.18)

Второе слагаемое тут зависит только от φ. Перенесём его в правую часть равенства.

(20.19)

Равенство возможно, когда обе части равны какой-то постоянной величине. Следовательно:

(20.20)

 

Решением этого уравнения являются функции

Угол φ может изменяться от 0 до 2π. Функция  должна быть периодической с периодом 2π. Это возможно, только если  Таким образом, из решения уравнения Шрёдингера получаем значение одного из квантовых чисел (конечно, из него можно получить их все). Число называется магнитным квантовым числом.

Далее, интегрируя квадрат модуля функции  от 0 до 2π и приравнивая полученное выражение к единице, получим, что 

Далее рассмотрим левую часть уравнения (1). Она, конечно, равна 

(20.21)

Разделим уравнение на 

(20.22)

После аналогичного вышеуказанному перенесению второго слагаемого в правую часть и обозначения величины, которой равны эти части, через  получаем

 

(20.23)

(20.24)

Решение этих двух последних уравнений приводит к значениям l и n соответственно. Три квантовых числа в совокупности полностью описывают состояния электрона в атоме водорода.

Модуль полной энергии электрона в стационарном состоянии в атоме водорода обратно пропорционален  Число n называется главным квантовым числом. Оно может иметь значения от 1 до  Его связь с энергией см. ниже.

Число l называется азимутальным квантовым числом и определяет орбитальный момент количества движения электрона и форму электронного облака; может иметь значения от 0 до n − 1 (n здесь относится к энергетическом уровню, на котором находится рассматриваемый электрон).

Магнитное квантовое число  определяет проекцию орбитального момента количества движения на выбранную ось в магнитном поле. Эта проекция равна