Возможные случаи пересечения криволинейныхВрезаповерхностей

ние

Возможные случаи пересечения криволинейныхКасаповерхностей

ние

K 2

K 3

Возможные случаи пересечения криволинейныхКасаповерхностей

ние

K 2

K 3

Теорема о

Еслидвойномдве поверхностикасании второго порядка имеют

двойное касание, то они пересекаются по двум

плоским кривым.

Примечание

Если оси пересекающихся поверхностей параллельны какой- либо плоскости проекций, то на эту плоскость кривые линии проецируются в прямые.

Теорема о двойном касании

Q1

P1

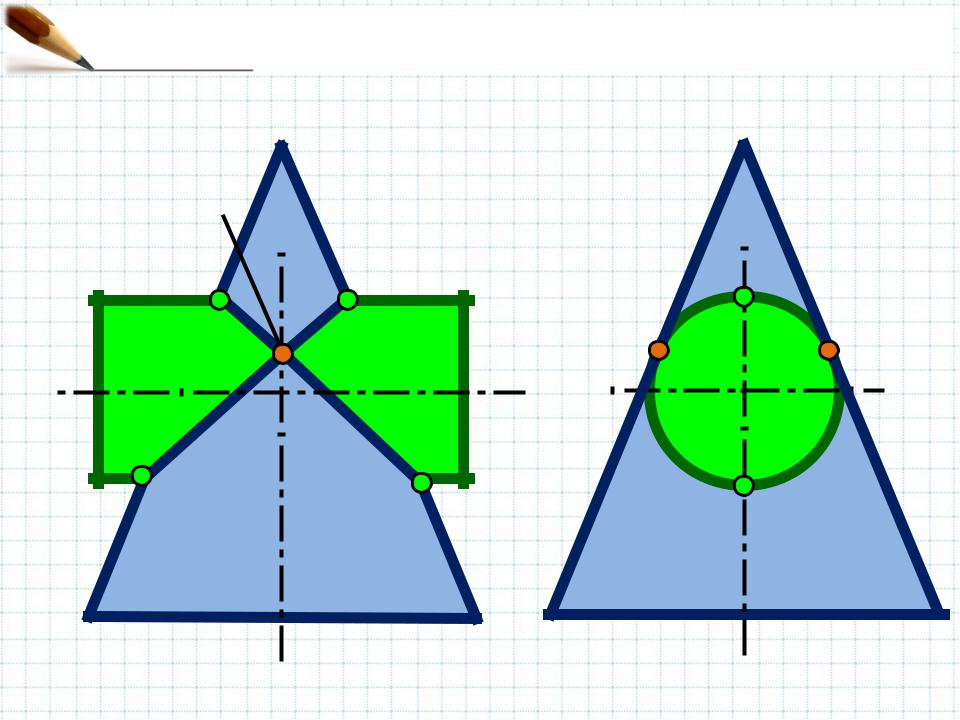
Теорема

Если двеМонжаповерхности второго порядка описаны или вписаны около третьей поверхности второго порядка, то они пересекаются по двум плоским кривым.

Теорема

Монжа

Теорема

Монжа

3

1

N

M

2

4