
4. Для извлечения корня n-й степени из комплексного числа используется вторая формула Муавра:
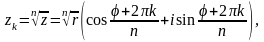
где
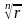 - арифметический корень из модуля
комплексного числа, k=0,
1, 2,…, n-1
- арифметический корень из модуля
комплексного числа, k=0,
1, 2,…, n-1
Пример.
Найти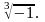
Решение:
Представим число –1 в тригонометрической форме:
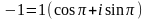
По второй формуле Муавра получаем:
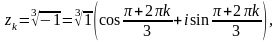
Получаем последовательно:
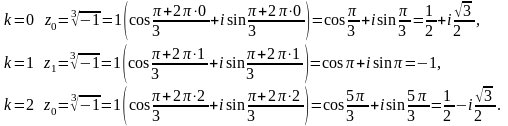
Геометрически все корни n-ой степени из комплексного числа лежат в углах правильного n-угольника, вписанного в окружность с центром в начале координат и радиуса .

Показательная форма комплексного числа.
Показательная и тригонометрические функции в области комплексных чисел связаны между собой формулой
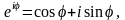
которая носит название формулы Эйлера. Обосновать ее можно с помощью теории степенных рядов.
Пусть комплексное число z в тригонометрической форме имеет вид . На основании формулы Эйлера выражение в скобках можно заменить на показательное выражение. В результате получим
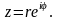
Эта запись называется
показательной формой комплексного
числа. Так же, как и в тригонометрической
форме, здесь

Действия над комплексными числами в показательной форме.
Действия над комплексными числами в показательной форме выполняются по правилам действий со степенями:

Решение уравнений с помощью комплексных чисел.
1. Решить квадратное уравнение
 .
.
Решение.
Вычислим дискриминант:

Дискриминант отрицателен, и в действительных числах уравнение решения не имеет. Но корень можно извлечь в комплексных числах:

По известным школьным формулам получаем два корня:
 –
сопряженные комплексные корни.
–
сопряженные комплексные корни.
2. Найти действительные
x
и y
из уравнения:
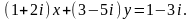
Решение.
В левой части уравнения раскроем скобки и сгруппируем действительные и мнимые слагаемые:
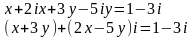
Воспользуемся условием равенства комплексных чисел:
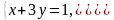
Расчет комплексных сопротивлений в электрических цепях переменного тока с помощью комплексных чисел.
В современной технике широко используют разнообразные по форме переменные токи и напряжения: синусоидальные, прямоугольные, треугольные и др. Значение тока, напряжения, ЭДС в любой момент времени t называется мгновенным значением и обозначается малыми строчными буквами, соответственно: i = i(t); u = u(t); e = e(t).
Токи, напряжения и ЭДС, мгновенные значения которых повторяются через равные промежутки времени, называют периодическими, а наименьший промежуток времени, через который эти повторения происходят, называют периодом Т.
Если кривая изменения периодического тока описывается синусоидой, то ток называют синусоидальным. Если кривая отличается от синусоиды, то ток несинусоидальный.
В промышленных масштабах электрическая энергия производится, передается и расходуется потребителями в виде синусоидальных токов, напряжений и ЭДС.
При расчете и анализе электрических цепей применяют несколько способов представления синусоидальных электрических величин: аналитический, временная диаграмма, графоаналитический, аналитический метод с использованием комплексных чисел.
Напомню уравнения для мгновенных значений силы тока, напряжения и ЭДС:
|
Im, Um, Em – амплитуды тока, напряжения, ЭДС; значение в скобках – фаза (полная фаза); φi, φu, φe – начальная фаза тока, напряжения, ЭДС; ω – циклическая частота, ω = 2π; – частота, = 1 / T; Т – период. |
Расчет линейных электрических схем гармонического (синусоидального) тока в установившемся режиме аналогичен расчету электрических схем постоянного тока. В обоих случаях составляют систему алгебраических уравнений по методам, основанным на законах Ома и Кирхгофа.
Для схем постоянного тока уравнения составляют по действительным значениям напряжений, токов, сопротивлений и проводимостей. В схемах же гармонического тока для алгебраизации интегрально-дифференциальных уравнений применяют комплексные (символические) величины: U, I, Z=R+ jХ (поскольку в электротехнике мгновенное значение силы тока обозначается i, то мнимую единицу обозначают буквой j). При этом все параметры записывают в виде комплексных чисел в алгебраической, показательной или тригонометрической форме. При переходе от интегрально-дифференциальных уравнений дифференцирование мгновенного значения заменяют умножением jω на соответствующую комплексную величину, а интегрирование — делением комплексной величины на jω:

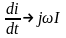
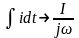
|
Синусоидальный ток
амплитуда силы тока Im – модуль комплексного числа, а угол φ являющийся начальной фазой, - аргумент комплексного числа. |
Использование комплексной формы представления позволяет заменить геометрические операции над векторами алгебраическими операциями над комплексными числами. В результате этого к анализу цепей переменного тока могут быть применены все методы анализа цепей постоянного тока.

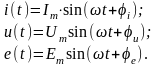

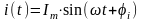 можно представить комплексным числом
Ím на комплексной
плоскости
можно представить комплексным числом
Ím на комплексной
плоскости
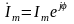 ,
где
,
где