Тема 1.2. Комплексные числа

Из истории возникновения комплексных чисел.

Для решения многих задач физики, электротехники и других наук оказалось недостаточно множества действительных чисел. Решение этих задач приводит к квадратным уравнениям с отрицательным дискриминантом. Эти уравнения не имеют решения в области действительных чисел. Но решение многих таких задач имеет вполне определенный физический смысл.

Одна из причин, которая приводит к необходимости расширения множества действительных чисел, связана с решением квадратных уравнений. Для того, чтобы сделать возможной операцию извлечения квадратного корня из любого действительного числа. Это, однако, не является достаточным основанием для того, чтобы вводить в математику новые числа. Оказалось, что если производить вычисления по обычным правилам над выражениями, в которых встречаются квадратный корень из отрицательного числа, то можно прийти к результату, уже не содержащему квадратный корень из отрицательного числа.

Впервые новые величины появились в известном труде «Великое искусство, или об алгебраических правилах» Джероламо Кардано (1545), в рамках формального решения задачи по вычислению двух чисел, которые в сумме дают 10, а при перемножении дают 40. Он получил для этой задачи квадратное уравнение для одного из слагаемых, и нашёл его корни: .

В комментарии к решению он написал: «Эти сложнейшие величины бесполезны, хотя и весьма хитроумны» и «Арифметические соображения становятся все более неуловимыми, достигая предела столь же утонченного, сколь и бесполезного».

Выражения вида 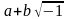, появляющиеся при решении квадратных и кубических уравнений, стали называть «мнимыми» с подачи Декарта, который называл их так, отвергая их реальность. И для многих других крупных ученых XVII века природа и право на существование мнимых величин представлялись весьма сомнительными, так же как сомнительными в то время считали и иррациональные числа, и даже отрицательные величины.

Символ 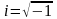предложил академик Петербургской академии наук Леонард Эйлер (1777), взявший для этого первую букву латинского слова imaginarius (воображаемый). Немецкий математик Карл Гаусс ввёл в широкое употребление термин «комплексное число» в 1831 году, хотя этот термин ранее использовал в том же смысле французский математик Лазар Карно в 1803 году.

Основные понятия

Определение. Комплексным числом z называется число вида ,

где a и b – действительные числа,

_i – мнимая единица, удовлетворяющая условию

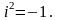
Число a называется действительной частью (Re z) комплексного числа z,

число bi называется мнимой частью (Im z) комплексного числа z.

Множество комплексных чисел обозначается буквой С.

_{Заметим, что множество} R действительных чисел содержится в множестве комплексных чисел С:

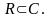
_{Всякое действительное} число а можно рассматривать как комплексное число вида

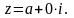
Числа 0 и 1 записываются соответственно:

При а=0 комплексное число обращается в число bi, которое называется чисто мнимым.

Запись комплексного числа в виде называется алгебраической формой записи комплексного числа.

Определение. Два комплексных числа 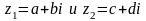называются равными, если, соответственно, равны их действительные части и коэффициенты при мнимой единице, т.е. а=с, b=d.

_{Определение.} Два комплексных числа называются взаимно сопряженными, если их действительные части равны, а мнимые отличаются знаками, т.е.

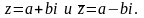
Определение. Комплексные числа вида называются противоположными.