2. Истечение газа из бака

2.1 Определение скорости истечения

Применим полученные формулы для решения вопроса об истечении газа из бака.

В нутри бака все параметры имеют значения параметров заторможенного газа. Через p, , T, M обозначим соответствующие параметры в выходном сечении, площадь которого S, и через – давление в камере, куда переходит истечение (это давление в теории истечения называют противодавлением). Для определения скорости истечения V воспользуемся уравнением

,

в котором отбросим индекс «1», а индекс «2» заменим «0».

Полагая V₀ = 0, получим:

,

откуда скорость истечения

.

Вынося за скобки p₀/₀ и считая процесс адиабатическим и изэнтропическим, то есть получим формулу Сен-Венана и Вантцеля

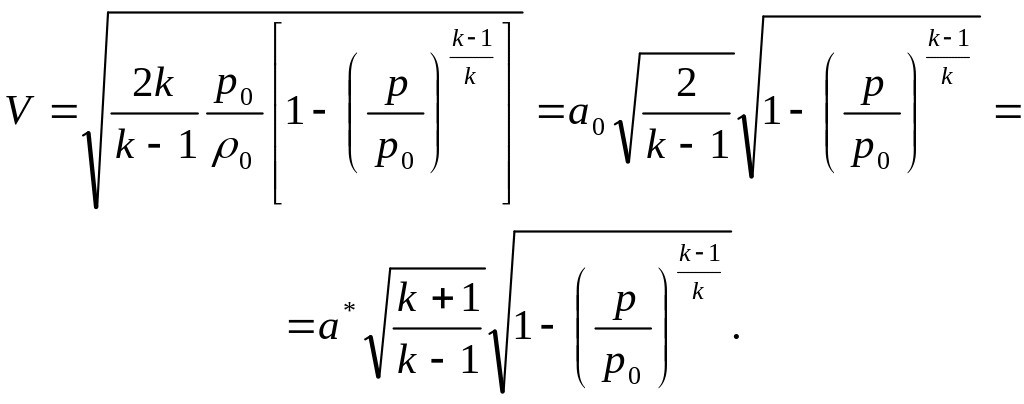(2.9)

Из (2.9) видно, что скорость при заданных параметрах заторможенного газа будет расти с уменьшением давления p.

2.2. Максимальная и критическая скорости

Скорость истечения через сопло будет максимальной при истечении в абсолютный вакуум (р = 0; Т = 0).

Сверхзвуковую скорость V_max при p = 0 определяют по формуле

. (2.10)

Это максимальная сверхзвуковая теоретическая скорость, которую можно получить лишь при истечении через насадок, поперечное сечение которого вначале уменьшается, а затем возрастает (сопло Лаваля).

Для воздуха, имеющего Т = 288 К и находящегося при атмосферном давлении максимальная скорость истечения в вакуум, V_max=760 м/с.

Рассмотрим истечение газа через сужающийся насадок. Используем формулу

откуда

.

Из последнего выражения следует, что при заданных параметрах заторможенного газа с увеличением скорости истечения скорость звука в движущемся газе убывает. Следовательно, при сужающемся насадке и достаточно большой разности давлений в баке и вне его, скорость V может достигнуть местной скорости звука. Дальнейшее уменьшение не может привести к увеличению V, так как внутренний объем бака окажется недоступен для внешних возмущений, поскольку он будет заперт потоком со звуковой скоростью. Максимальная скорость истечения через сужающийся насадок будет равна критической скорости, определяемой из следующих соотношений:

,

откуда

.

Отношение

показывает, что действительная (наибольшая) скорость истечения через сужающийся насадок будет в раз меньше определенной по формуле (2.10) максимальной скорости.

Определим расход газа через сужающееся сопло. При докритическом режиме масса газа, вытекающего из бака за одну секунду равна . Критическое значение этой массы . Отношение этих масс даст безразмерный расход, т.е. отношение произвольного расхода к его критическому значению

, (2.11)

где , .

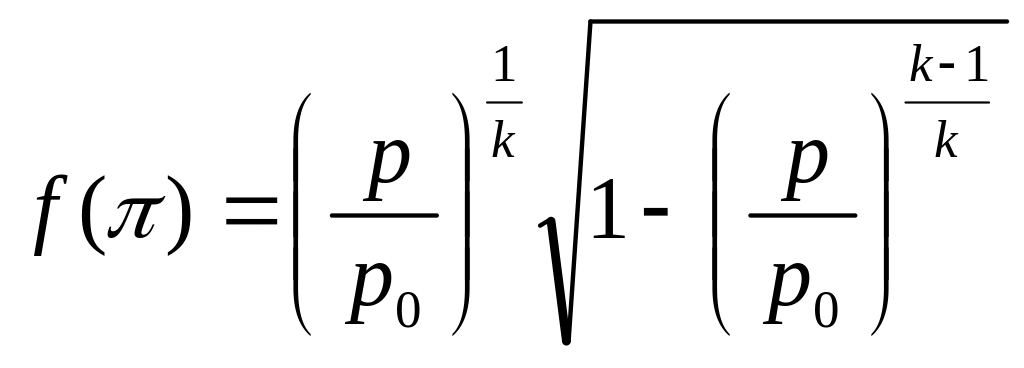На рисунке представлен график зависимости от отношения противодавления к давлению в баке p₀. До тех пор, пока давление на выходе из сопла p не станет равным критическому , противодавление будет совпадать с p, и кривая определится соотношением (2.11) (правая сплошная ветвь кривой).

П ри дальнейшем уменьшении противодавления при , наступит «запирание» выходного сечения, и истечение будет происходить с постоянной критической скоростью , несмотря на снижение . Часть графика, соответствующая интервалу (для воздуха ), представится сплошной горизонтальной прямой, а не пунктирной спадающей кривой, как это следовало бы по (2.11). Максимально возможный при заданных параметрах в баке расход газа через сужающееся сопло равен критическому расходу и определится с учетом формул (2.8)

Массовый докритический расход определится формулой

.

При подсчете секундного расхода газа через сопло удобно пользоваться приведенным секундным расходом q(M), который является функцией числа Маха и определяется по зависимостям:

или

,

где S^* – площадь критического сечения сопла; S – площадь сечения, в котором достигается скорость V.

Приведенный секундный расход выражается также через отношение давлений :

,

где – газодинамическая функция.

Секундный расход (для воздуха) можно рассчитать по формулам:

, если > 0,528p₀;

, если < 0,528p₀,

где S – площадь выходного сечения сопла.