3. Критерий Найквиста.

Комплексный спектр дискретной передаточной функции называют частотной передаточной функцией дискретной системы (звена).

Так как , где - дискретная передаточная функция прямого канала системы с единичной отрицательной обратной связью, то .

В этом случае

где n - общее число корней;

m - число корней характеристического уравнения разомкнутой системы

по модулю больше 1.

Формулировка критерия Найквиста №1

Для того чтобы замкнутая система была устойчивой, необходимо и достаточно, чтобы при изменении ω от 0 до вектор F(z) равный 1+W(z) имел приращение аргумента m, где m - число корней характеристического уравнения разомкнутой цифровой системы, лежащих вне круга единичного радиуса.

Пример 1 Пример 2

Формулировка критерия Найквиста №2

Для того чтобы замкнутая система была устойчивой, необходимо и достаточно, чтобы при изменении ω от 0 до амплитудно-фазовая характеристика разомкнутой системы охватывала точку с координатами (-1,j0) m/2 раз против часовой стрелки, где m - число корней характеристического уравнения разомкнутой системы по модулю > 1.

Формулировка критерия Найквиста для ЛПЧХ совпадает с формулировкой для непрерывных систем.

Устойчивость разомкнутого контура цифровой системы определяется устойчивостью её непрерывной части: если последняя устойчива, то и весь разомкнутый контур (включая импульсный элемент) устойчивы.

4. Критерий Гурвица.

Формулировка критерия Гурвица для непрерывных систем справедлива и для дискретных систем, если в характеристическом уравнении системы произвести замену .

Введем комплексную переменную w, связанную с комплексной переменной z билинейным преобразованием:

, где , относительная безразмерная

псевдочастота.

Тогда, произведя замену в характеристическом полиноме | , получим характеристический полином , по которому определим устойчивость системы по критерию Гурвица.

При изменении частоты в пределах относительная псевдочастота пробегает все значения от - до +, а комплексная переменная w движется по оси мнимых чисел от -j до +j. Внутренняя часть круга единичного радиуса отображается при этом на левую полуплоскость.

При помощи w - преобразования осуществляется конформное отображение внутренности окружности единичного радиуса на плоскости z в левую полуплоскость w. При этом контур окружности единичного радиуса переходит в мнимую ось плоскости w.

При исследовании дискретных систем по преобразованным при помощи w - преобразования передаточным функциям могут использоваться обычные приемы и критерии, справедливые для непрерывных систем, в том числе и критерий Гурвица.

Логарифмические псевдочастотные характеристики цифровых систем

Осуществим подстановку в W(z) , ,

где - относительная безразмерная псевдочастота.

Введем понятие абсолютной псевдочастоты :

, с^-1; ;

.

При малых углах , тогда при выполнении условия можно в расчетах заменить псевдочастоту действительной круговой частотой, что может быть использовано, в частности, при расчетах реакции ЦАС на медленно меняющиеся гармонические сигналы на входе.

Получим псевдочастотную передаточную функцию разомкнутой цифровой системы

/ = , здесь соответствует р непрерывной системы, поэтому ЛПЧХ строятся по правилам для непрерывных систем. Затем применяется критерий устойчивости Найквиста для ЛЧХ.

Пример 1. Пусть - интегратор; , .

yцап[n]

yцап(t)

.

Тогда .

Чтобы перейти к логарифмическим частотным характеристикам произведем подстановку : , если вместо w подставить , получим псевдочастотную функцию : .

- комплексный передаточный коэффициент интегрирующего звена с фиксатором 0-го порядка.

Свойства :

1. C уменьшением периода дискретизации (T0, =2/T ) характеристика приближается к характеристике непрерывной системы;

2. Предельный фазовый сдвиг равен -, такая замкнутая система приближается к границе устойчивости при больших k.

Пример 2.

Пусть , тогда

,

где .

.

Перейдем к псевдочастотным функциям :

,

так как . (1)

Исследуем это выражение :

1. Пусть период дискретности [ ] и определим :

, это видно из выражения (1), отсюда , при этих соотношениях .

- неминимально - фазовый множитель.

2. Пусть , тогда , .

.

Построим частотные характеристики:

1. 2.

Пример 3.

Построить логарифмические псевдочастотные характеристики системы, если передаточная функция непрерывной части имеет вид

.

Экстраполятор нулевого порядка.

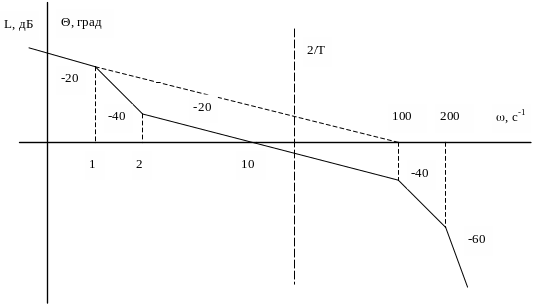
Зададим период дискретности T=0.1с. На графике отложим частоту , выделим НЧ и ВЧ части характеристики;

, .

Теперь запишем выражение для псевдочастотной функции:

На основании этого выражения построим ЛПЧХ, где .

Замечание: фазовые характеристики непрерывных и цифровых систем существенно различаются.