Решение систем дифференциальных уравнений.

 задача Коши заключается в решении системы обыкновенных дифференциальных уравнений первого порядка, представленных в виде:

(19)

где j=1N – номер каждой зависимой переменной y_j, x – независимая переменная.

Задача Коши сводится к интегрированию дифференциальных уравнений. Порядок метода численного интегрирования определяет и порядок метода решения системы дифференциальных уравнений. Обобщенная форма записи каждого из уравнений системы может быть представлена в общем виде:

, (20)

где Y_j в правой части уравнений – это векторы переменных y₁, y₂, …,y_j, …,y_N, а F_j - правая часть каждого из уравнений. В частности, одно дифференциальное уравнение записывается в виде dy/dx=F₁(x,y). Дифференциальные уравнения высшего порядка:

, (21)

где n - порядок уравнения, и уравнения (16) могут быть сведены к системам представленного ранее вида с помощью следующих преобразований:

…..

(22)

Таким образом, решение уравнения сводится к решению системы дифференциальных уравнений первого порядка.

 модифицированный метод Эйлера второго порядка выражается следующими рекурентными формулами:

где (23)

. (24)

Метод дает погрешность R~(h³) и имеет меньшее время вычислений, так как вместо нескольких итераций производится вычисление только одного значения .

 метод трапеций – одна из модификаций метода Эйлера второго порядка. Он реализуется применением на каждом шаге формулы:

, (25)

где k_j1=hF_j(x_i,Y_ji), (26)

k_j2=hF_j(x_i+h,Y_ji+k_ji), (27)

дает погрешность R~(h³). Этот метод относится к общим методам Рунге-Кутта.

 метод Рунге-Кутта четвертого порядка является наиболее распространенным методом решения системы дифференциальных уравнений при постоянном шаге h=Const. Его достоинством является высокая точность ( R~h⁵) и меньшая склонность к возникновению неустойчивости решения.

Алгоритм реализации метода Рунге-Кутта заключается в циклических вычислениях Y_j(i+1) на каждом (i+1) шаге по следующим формулам:

(28)

При переходе от одной формулы к другой задаются или вычисляются соответствующие значения x, Y_j и находятся по подпрограмме значения функций F_j(x,Y_j).

Решение одного дифференциального уравнения методом Рунге-Кутта производится по приведенным выше формулам, если в них опустить индекс j, а из алгоритма исключить циклы. Последнее значительно упрощает программу и позволяет получить минимально возможное время счета. Метод Рунге-Кутта, используемый для решения дифференциального уравнения второго порядка вида и имеющий погрешность R~h⁵, реализуется следующими уравнениями:

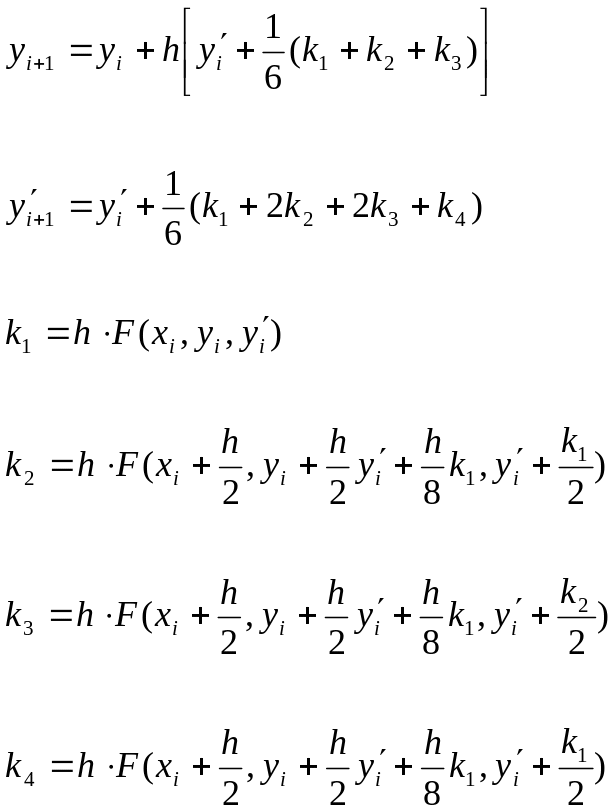(29)

Перед началом вычислений необходимо задать шаг h и начальные значения x₀, y(x₀)=y₀, .

 метод Рунге-Кутта с автоматическим изменением шага заключается в изменении шага h после вычисления Y_j(i+1) на шаг h/2 и повторное вычисление уже Y^*_j(i+1). Если условие |Y_j(i+1) – Y^*_j(i+1)|<, то вычисления продолжают с шагом h, если условие не выполняется, то шаг уменьшают. Метод обеспечивает приближенную оценку погрешности на каждом шаге интегрирования (R~h⁵).

Все описанные методы относятся к одношаговым методам, они обеспечивают автоматическое начало вычислений при заданных начальных условиях и изменение (в том числе автоматическое) шага в ходе вычислений. Многочисленные методы решения дифференциальных уравнений базируются на использовании данных решения на нескольких предшествующих шагах. Это повышает скорость вычислений, но, для начала вычислений приходится выполнять одношаговыми методами несколько первых шагов.