
- •Тема 12. Многогранники. Коло і круг
- •12.1. Ламана. Многокутник
- •12.2. Коло та круг
- •12.2.1. Основні поняття
- •12.2.2. Довжина кола. Центральний кут і дуга кола
- •12.2.3. Кути, вписані у коло
- •12.2.4. Кола, вписані та описані навколо трикутника
- •12.2.5. Зовнівписане коло
- •12.3. Чотирикутник
- •12.3.1. Паралелограм
- •12.3.2. Прямокутник
- •12.3.3. Ромб
- •12.3.4. Квадрат
- •12.3.5. Трапеція
- •12.3.6. Вписані та описані чотирикутники
- •12.3.7. Правильні многокутники
- •12.3.8. Площі чотирикутників та правильних багатокутників
- •12.4. Площа круга, кругового сектора і кругового сегмента
12.4. Площа круга, кругового сектора і кругового сегмента
Кругом називається фігура, яка складається з усіх точок площини, що лежать від даної точки на відстані, не більшій за дану. Ця точка називається центром круга, а дана відстань – радіусом круга.
Межею крута є коло з тим самим центром і радіусом, тому круг можна означити як частину площини, обмежену колом.
Площа крута обчислюється за формулою:
![]() ,
,
де R і D – радіус і діаметр круга.
Круговим сектором називається частина крута, що лежить усередині відповідного центрального кута (мал. 12.32). Площа кругового сектора обчислюється за формулою:
![]() ,
,
де R – радіус круга, а – градусна міра відповідного центрального кута.
Круговим сегментом називається спільна частина круга і півплощини, межа якої містить хорду кола (мал. 12.33).
|
|
|
Рис. 12.32 |
Рис. 12.33 |
|
Площа сегмента, що не дорівнює півкругу, обчислюється за формулою:
![]() ,
(*)
,
(*)
де
– градусна міра центрального кута, який
містить дугу цього кругового сегмента,
а
![]() – площа трикутника з вершинами в центрі
круга й кінцях радіусів, що обмежують
відповідний сектор. Знак “-”
треба брати тоді, коли
– площа трикутника з вершинами в центрі
круга й кінцях радіусів, що обмежують
відповідний сектор. Знак “-”
треба брати тоді, коли
![]() ,
а знак “+”
–
тоді, коли
,
а знак “+”
–
тоді, коли
![]() .
.
Оскільки
![]() ,
то формулі (*) можна надати
вигляду
,
то формулі (*) можна надати
вигляду
![]() (**).
(**).
Якщо відповідний кут сегмента
виразити в радіанній мірі
![]() ,
то формула (**)
спрощується:
,
то формула (**)
спрощується:
![]() .
.
|
Приклади |
Приклад 12.1. З точки кола проведено дві хорди, рівні радіусу. Знайти кут між ними.
|
Рис. 12.34 |
|
На
рис. 12.34
показано хорди АВ
і АС,
кожна з яких дорівнює радіусу кола.
Трикутники АBО
і АСО
рівносторонні, отже, матимемо:
![]() ,
,
![]() .
Відповідь:
.
Відповідь:
![]() .
.
Приклад 12.2. Висота і менша діагональ ромба дорівнюють відповідно h і d. Знайти площу ромба.
|
Рис. 12.35 |
|
Нехай
ВЕ
– висота ромба ABCD
(рис.
12.35),
![]() ,
,
![]() – менша діагональ ромба.
– менша діагональ ромба.
З
![]() маємо
маємо
![]() .
Нехай
.
Нехай
![]() .
Тоді
.
Тоді
![]() .
З
.
З
![]() маємо:
маємо:
![]() ,
,
![]() ,
звідки
,
звідки
![]() ,
,
![]() .
Позначивши площу ромба через S,
маємо
.
Позначивши площу ромба через S,
маємо
![]() .
Відповідь:
.
Відповідь:
![]() .
.
|
Питання для самоперевірки |
Що називається ламаною лінією, її сторонами, вершинами?
Яка ламана називається замкненою? В якому випадку ламана утворює багатокутник?
Дайте означення плоского багатокутника, його сторонам, діагоналям, внутрішнього та зовнішнього кута.
Що називається колом, радіусом, діаметром, хордою?
Сформулюйте означення дотичної до кола. Яка точка є точкою дотику кіл? Запишіть властивість дотичних, проведених до кола з однієї точки.
Який відрізок називається лінією центрів?
Дайте означення концентричних кіл.
Які способи дотику кіл ви знаєте?
Запишіть властивість центрів кіл, що дотикаються.
Що називається центральним кутом? Чому дорівнює його градусна міра?
Дайте означення дуги кола. Чому дорівнює її градусна та радіанна міра?
Сформулюйте означення та властивості кутів, вписаних у коло.
Які кола вважаються вписаним та описаним навколо трикутника?
Чому дорівнюють радіуси вписаного і описаного кіл?
За яких умов коло називається зовнівписаним?
Запишіть співвідношення між радіусами зовніописаних кіл та висотами трикутника.
Який чотирикутник називається опуклим?
За яких умов можна навколо чотирикутника описати й у чотирикутник вписати коло?
Опишіть за схемою (означення, властивості елементів, формули площ) наступні чотирикутники:
паралелограм;
прямокутник,
ромб;
квадрат;
трапеція.
Який многокутник називається правильним, вписаним у коло, описаним навколо кола?
Чому дорівнюють наступні елементи правильного п-кутника ( при
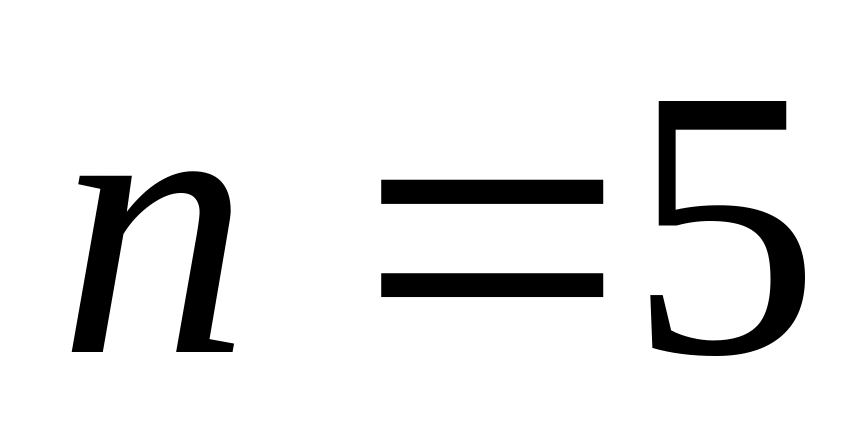 ,
,
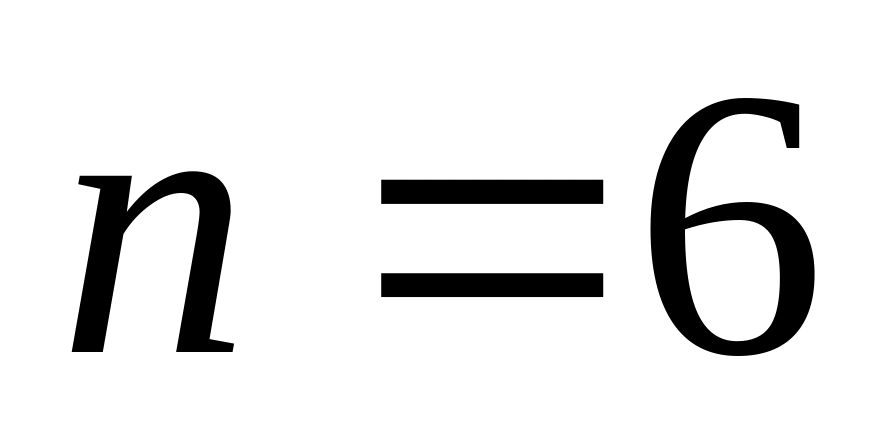 ,
,
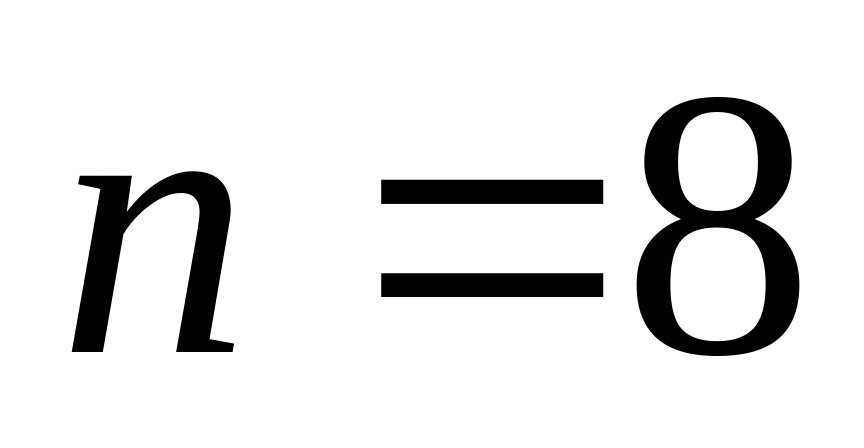 ,
,
 )
:
)
:кількість діагоналей;
кут між суміжними сторонами;
радіус вписаного кола;
радіус описаного кола.
Дайте означення і запишіть формули площ круга, кругового сектора, кругового сегмента.
|
Вправи |
Знайти діагональ і бічну сторону рівнобедреної трапеції з основами 20 і 12 см, якщо відомо, що центр описаного кола лежить на більшій основі трапеції.
У рівнобедреній трапеції дані основи а = 21 см,
 см і висота
см і висота
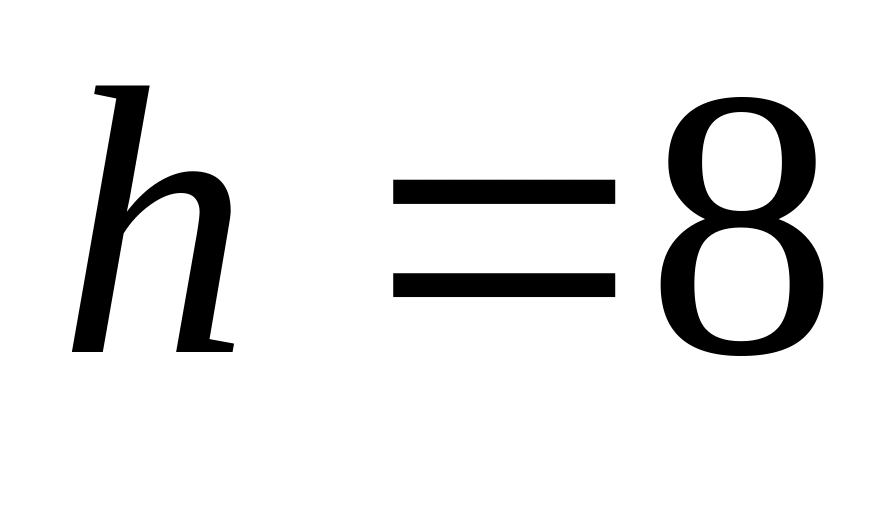 см. Знайти радіус описаного кола.
см. Знайти радіус описаного кола.Висота ромба, проведена з вершини тупого кута, поділяє його сторону на відрізки довжиною т и п. Визначити діагоналі ромба.
Дано квадрат, дві вершини якого лежать на колі радіуса
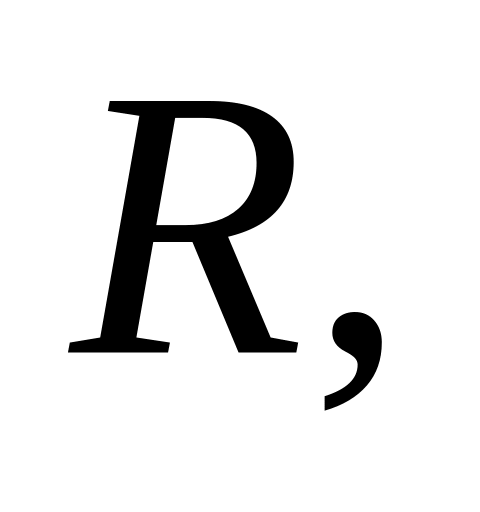 дві інші – на дотичній до цього кола.
Знайти довжину діагоналі квадрата.
дві інші – на дотичній до цього кола.
Знайти довжину діагоналі квадрата.У ромб, що ділиться своєю діагоналлю на два рівносторонніх трикутники, вписаного кола радіуса 2. Знайти сторону ромба.
З однієї точки проведені до кола дві дотичні. Довжина кожної дотичної 12 см, а відстань між точками дотику 14,4 см. Визначити радіус кола.
З точки А проведені дві прямі, що стосуються дотикаються до кола
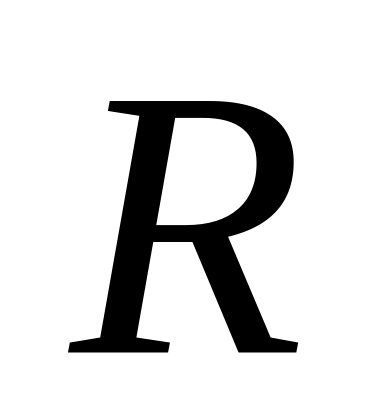 в точках В
и
С
так,
що трикутник АВС
– рівносторонній. Знайти його площу.
в точках В
и
С
так,
що трикутник АВС
– рівносторонній. Знайти його площу.Величина одного з кутів паралелограма дорівнює
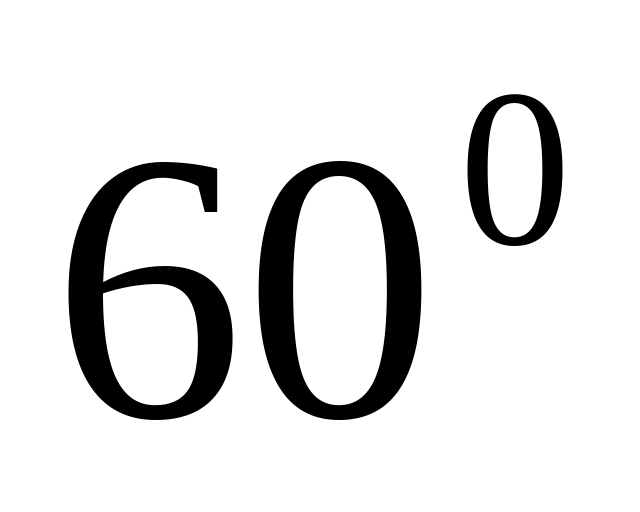 ,
а менша діагональ
,
а менша діагональ
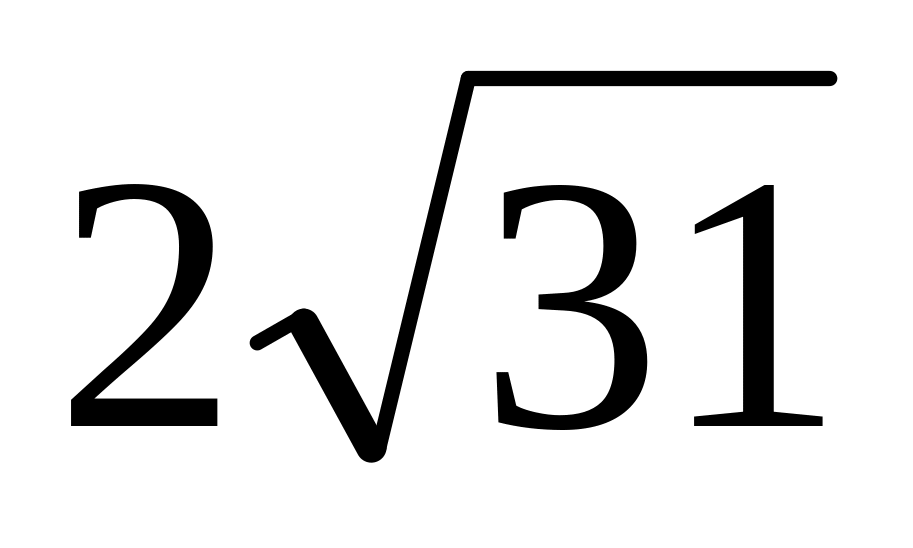 см. Довжина перпендикуляра, проведеного
з точки перетину діагоналей до більшої
сторони, дорівнює
см. Довжина перпендикуляра, проведеного
з точки перетину діагоналей до більшої
сторони, дорівнює
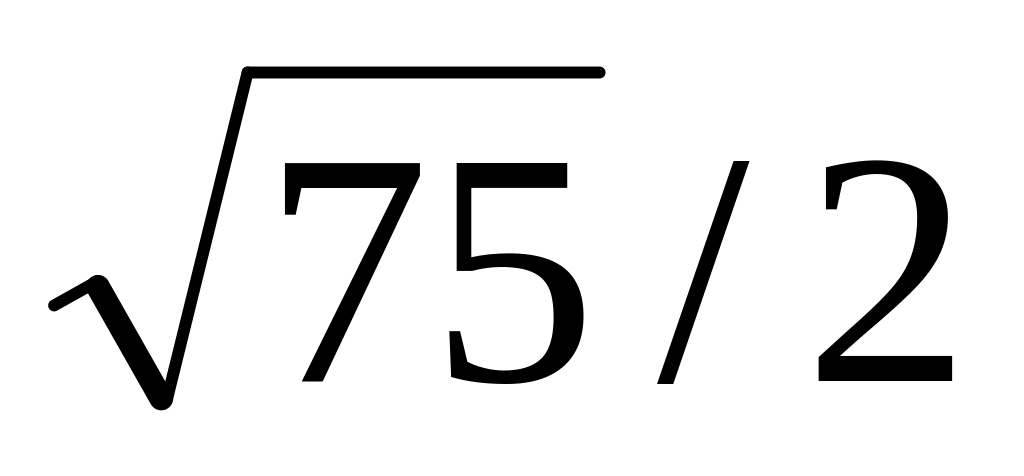 см. Знайти довжини сторін і більшої
діагоналі паралелограма.
см. Знайти довжини сторін і більшої
діагоналі паралелограма.Один з кутів трапеції дорівнює 300, а прямі, що містять бічні сторони трапеції, перетинаються під прямим кутом. Знайти довжину меншої бічної сторони трапеції, якщо її середня лінія дорівнює 10 см, а одна з основ 8 см.
У паралелограмі
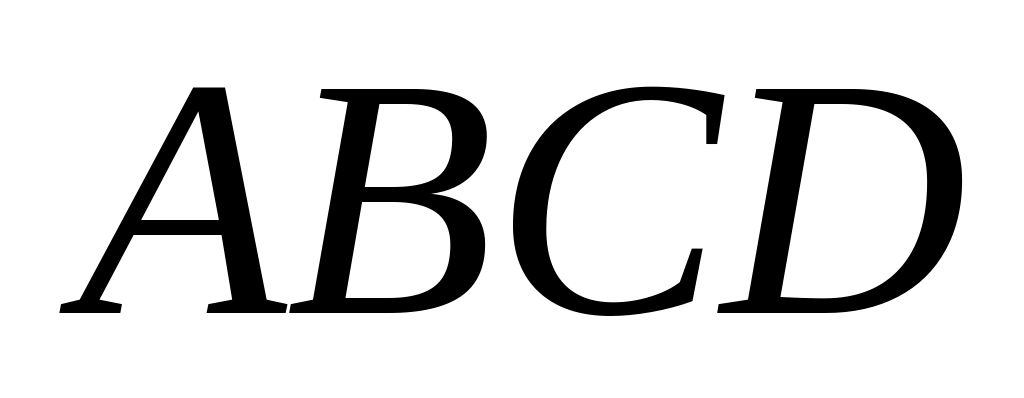 висота, проведена з вершини В
тупого кута на сторону
висота, проведена з вершини В
тупого кута на сторону
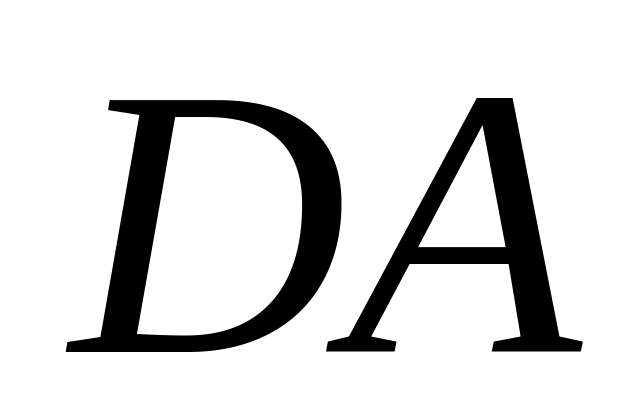 ,
ділить її у відношенні 5:3, рахуючи від
вершини
,
ділить її у відношенні 5:3, рахуючи від
вершини
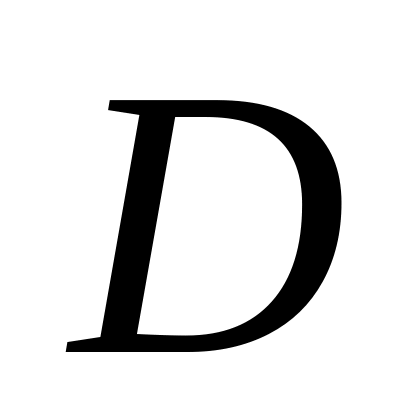 .
Знайти відношення
.
Знайти відношення
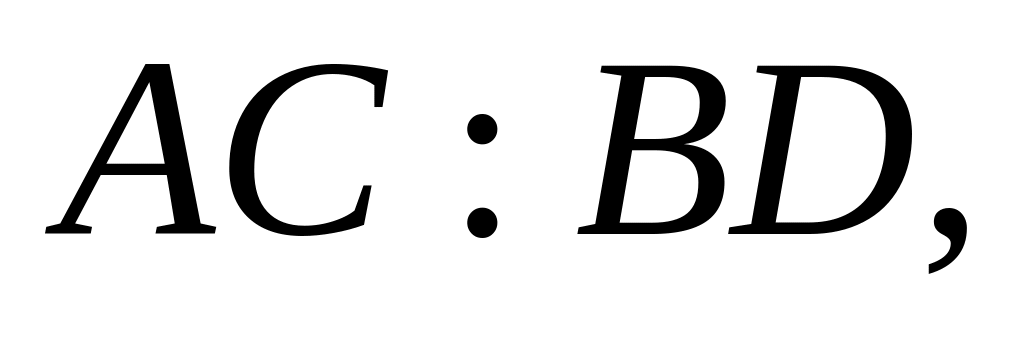 якщо
якщо
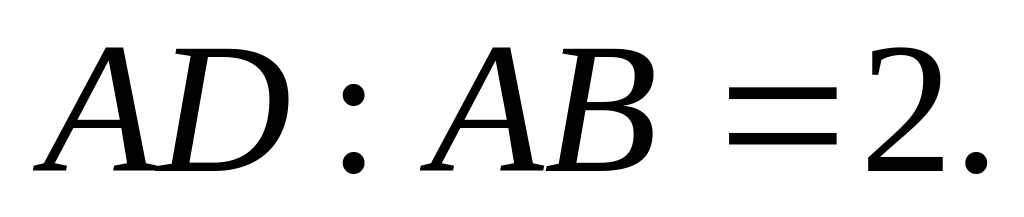
Знайти діагональ і бічну сторону рівнобедреної трапеції з основами 20 і 12 см, якщо відомо, що центр описаного кола лежить на більшій основі трапеції.
У рівнобедреній трапеції дані основи
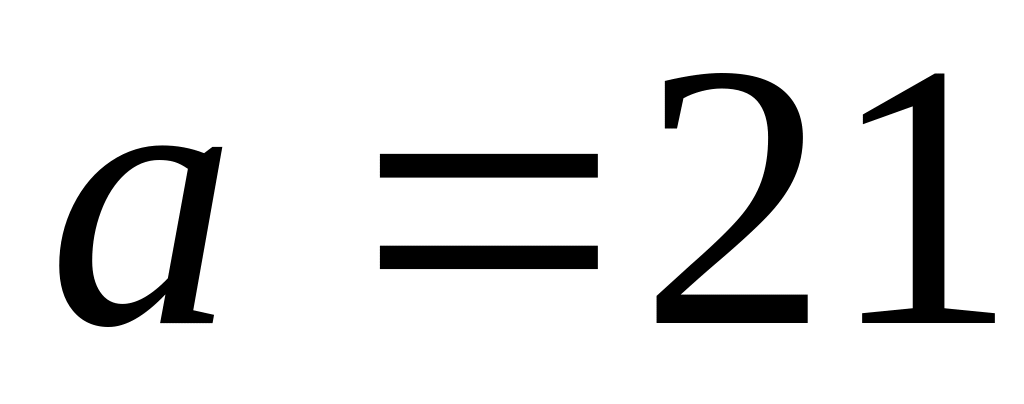 см,
см,
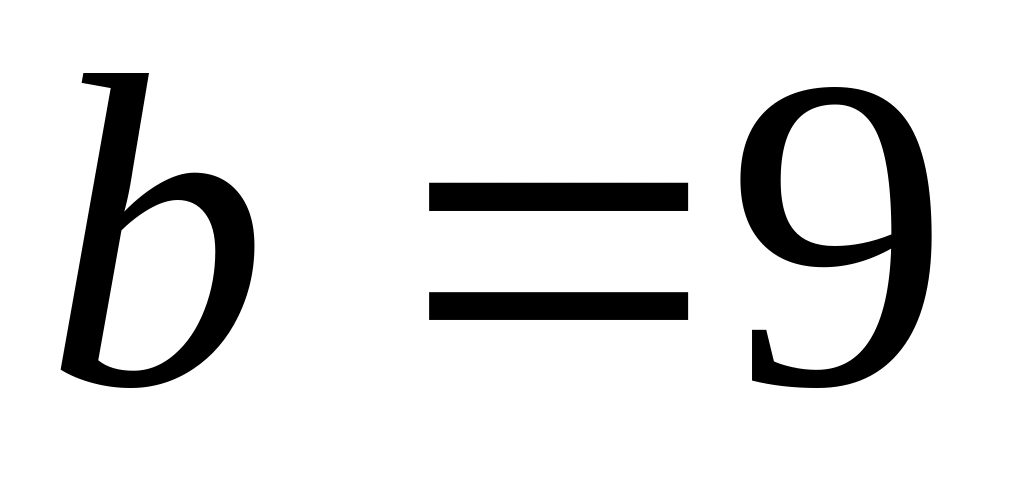 см і висота
см і висота
 см знайти радіус описаного кола.
см знайти радіус описаного кола.Висота ромба, яка проведена з вершини тупого кута, поділяє його сторону на відрізки довжиною т и п. Визначити діагоналі ромба.






