12.3.4. Квадрат

Квадрат – це прямокутник, у якого всі сторони рівні між собою (рис. 12. 29).

У квадраті всі кути прямі.

Рис. 12.29

Діагоналі квадрата однакові і більші від його сторони в рази:

.

Радіуси вписаного і описаного кіл дорівнюють

.

12.3.5. Трапеція

Трапеція – це чотирикутник, у якого тільки дві протилежні сторони паралельні. Ці паралельні сторони називаються основами трапеції (а і b на рис. 12.30). Дві інші сторони (с і d) називаються бічними сторонами. Трапеція, у якої бічні сторони рівні, називається рівнобічною.

Рис. 12.30

Відрізок, що сполучає середини бічних сторін трапеції, називається середньою лінією трапеції. Середня лінія трапеції l паралельна її основам, дорівнює їх півсумі і ділить висоту трапеції на два рівних відрізки:

.

Трапецію можна вписати в коло тоді і тільки тоді, коли вона рівнобічна.

Якщо в рівнобічну трапецію можна вписати коло радіусом r, то

,

де а і b – основи трапеції, с – бічна сторона, l – середня лінія.

Таким чином, з розглянутих чотирикутників коло можна вписати в ромб, квадрат і трапецію, сума основ якої дорівнює сумі бічних сторін.

12.3.6. Вписані та описані чотирикутники

У чотирикутник можна вписати коло тоді й тільки тоді, коли суми протилежних сторін рівні, виконується рівність . З усіх паралелограмів лише в ромб (зокрема, у квадрат) можна вписати коло.

Навколо чотирикутника можна описати коло тоді й лише тоді, коли суми протилежних кутів рівні, тобто має місце рівність . З усіх паралелограмів лише навколо прямокутника (зокрема, квадрата) можна описати коло. Навколо трапеції можна описати коло за умови, що вона рівнобічна. Для вписаного чотирикутника справедливі формули:

.

12.3.7. Правильні многокутники

Опуклий многокутник називається правильним, якщо в нього всі сторони рівні між собою й усі кути однакові.

Многокутник називається вписаним у коло, якщо всі його вершини лежать на деякому колі. Многокутник називається описаним навколо кола, якщо всі його сторони дотикаються до якогось кола. На рис. 12. 31 показано шестикутник, у який вписано коло і навколо якого описано коло.

Рис. 12.31

Теорема 12.13. Правильний опуклий многокутник є вписаним у коло й описаним навколо кола.

Нехай у правильному многокутнику a – сторона, n – кількість сторін.

Тоді:

1) кількість діагоналей n-кутника дорівнює

;

2) кут між суміжними (сусідніми) сторонами правильного n-кутника дорівнює

;

3) радіуси вписаного й описаного кіл дорівнюють

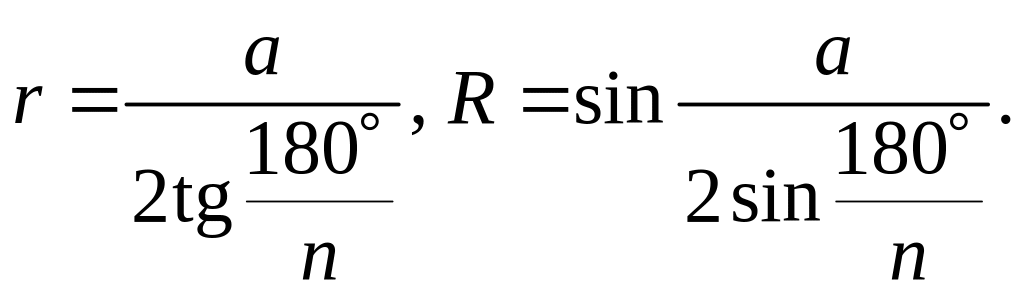
У правильному шестикутнику , отже,

Кут між суміжними сторонами правильного шестикутника дорівнює

.

У правильному восьмикутнику :

; ; .

де а – сторона восьмикутника.

У правильному десятикутнику :

; ; ,

де а – сторона десятикутника.

12.3.8. Площі чотирикутників та правильних багатокутників

Введемо наступні позначення: і – діагоналі, – кут між діагоналями, а, b – суміжні сторони, – кут між сторонами а і b, – висота, опущена на сторону а, S – площа.

1. Площа паралелограма .

2. Площа прямокутника .

3. Площа ромба .

4. Площа квадрата .

5. Площа трапеції , де l – середня лінія трапеції.

6. Площа правильного багатокутника або , де а – сторона, n – кількість сторін многокутника.

7. Площа правильного п’ятикутника .

8. Площа правильного шестикутника .

9. Площа правильного восьмикутника .

10. Площа правильного десятикутника .