12.2.5. Зовнівписане коло

Коло називається зовнівписаним у трикутник, якщо воно лежить зовні його, дотикається до однієї зі сторін трикутника і до прямих, на яких лежать інші сторони (мал. 12.25).

Якщо – кут, що лежить проти сторони a трикутника, тоді радіус кола, зовнівписаного до цієї сторони, можна обчислити за формулами

,

де р – півпериметр трикутника, r – радіус вписаного кола. Так само і для решти радіусів зовнівписаних кіл ( , ).

Рис. 12.25

Між радіусами вписаного кола, зовнівписаних кіл і висотами трикутника існує співвідношення

.

12.3. Чотирикутник

Розглядаємо тільки опуклі чотирикутники, тобто такі, для яких відрізок, що сполучає будь-які дві його точки, повністю належить цьому чотирикутнику (рис. 12.26).

Нехай: а і b, b і с, с і d, d і а – суміжні сторони; , , , – кути між суміжними сторонами; а і с, b і d – протилежні сторони.

Рис. 12.26

У чотирикутник можна вписати коло тоді і тільки тоді, коли суми протилежних сторін рівні між собою: .

Для вписаного у коло чотирикутника справедлива формула:

,

де i – діагоналі чотирикутника.

Навколо чотирикутника можна описати коло тоді і тільки тоді, коли сума протилежних кутів дорівнює 180°: , .

Якщо навколо чотирикутника описано коло, то цей чотирикутник буде вписаним у коло.

12.3.1. Паралелограм

Паралелограм – це чотирикутник, у якого протилежні сторони лежать на паралельних прямих (рис. 12. 27).

У паралелограмі:

• протилежні сторони рівні між собою: ;

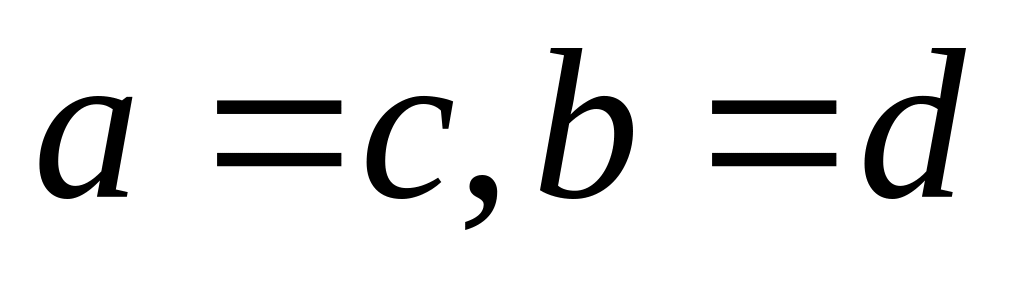• протилежні кути рівні між собою: ;

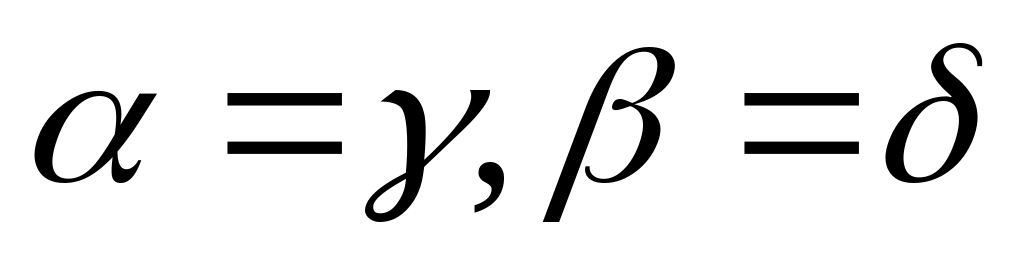• сума кутів, прилеглих до однієї (будь-якої) сторони паралелограма дорівнює 180°:

.

а)	б)
Рис. 12.27

У паралелограмі сума квадратів діагоналей дорівнює подвоєній сумі квадратів суміжних сторін:

.

Діагоналі паралелограма і (рис. 12. 27, б) обчислюються за формулами:

де – гострий кут паралелограма.

Паралелограм можна вписати в коло тоді і тільки тоді, коли він є прямокутником.

У паралелограм можна вписати коло тоді і тільки тоді, коли він є ромбом.

12.3.2. Прямокутник

Прямокутник – це паралелограм, у якого всі кути прямі (рис. 12.28).

Рис. 12.28

У прямокутнику протилежні сторони рівні., між собою:

.

Діагоналі прямокутника рівні між собою і обчислюються за формулою:

.

Периметр прямокутника дорівнює подвоєній сумі його суміжних сторін:

.

Навколо прямокутника завжди можна описати коло. Радіус описаного кола дорівнює половині діагоналі прямокутника:

.

12.3.3. Ромб

Ромб – це паралелограм, у якого всі сторони рівні між собою (рис. 12.29).

Рис. 12.28

У ромбі протилежні кути рівні між собою.

Діагоналі ромба взаємно перпендикулярні і є бісектрисами кутів ромба.

Діагоналі ромба обчислюють за формулами:

,

де a – сторона, – гострий кут ромба.

У ромб можна вписати коло. Радіус вписаного кола дорівнює

,

де – гострий кут ромба, – висота ромба.