2.2, 2.3, 2.4 Модель Кронига-Пенни.

В модели Кронига-Пенни рассматривая движение электрона в линейной цепочке прямоугольных потенциальных ям.

Уравнение Шредингера:

Решение для обл. I (U=0) 1(x)=Aeiαx+Be-iαx

Решение для обл. II (U=U0) 2(x)=Ceβx+De-βx

; ;

A, B, C, D – постоянные коэффициенты.

1(x)=U(x)eikx

P=mabU₀/ℏ²; P – проницаемость барьера (безразмерная величина).

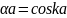Для реальных тв. тел P>>1. 1. P→kn; P>>1, по kn. 2. P→∞; Px→(0÷1). Надо, чтобы x→0, тогда разрешены не все Е, а только определенные. 3. P→0; cos ; ; разрешены все значения k.

Рис.2. Зависимость левой части уравнения (1) от αa. Движение по оси αa приводит к образованию 1-ой, 2-ой… запрещенной зон. Наблюдается чередование запрещ. (незаштрих.) и разрешенных(заштрих)

зон. По мере увелич. номера запр. зоны ширина запр. зоны уменьш, а ширина разреш. зоны увел.

P=∞ получаем вертикальные линии (дискретные значения Е).

Рисунок 3. Зависимость ε(k) для электрона в одномерной решетке.

Энергия растет с ростом волнового вектора.

На границе зон производная (dE/dK)_гр=0. E(K) вблизи границ зон явл. квадратичной функцией волнового вектора К, отсчитанного от этих границ: E=E₀+AK², E₀- энергия на границе зоны.

Рисунок 4. Зависимость E(k) в пред­ставлении приведенных зон

2.5 Методы изображения энергетических диаграмм твердых тел: металлы, полупроводники, диэлектрики.

Энергетическая диаграмма вещества показывает преобразования энергии в веществе.

Рис. 1 «Энергетические диаграммы металлов(а), полупроводников(б) и диэлектриков(в) при Т=0 К»

Из рисунка видно, что по характеру заполнения зон электронами все тела можно разделить на две большие группы:

• к первой группе относят тела, у которых над целиком заполненными зонами расположена зона, заполненная лишь частично (рис. 1, а). Такая зона возникает в том случае, когда атомный уровень, из которого она образуется, заполнен в атоме не полностью. Наличие зоны, заполненной лишь частично, присуще металлам. У металлов запрещенная зона отсутствует;

• ко второй группе относят тела, у которых над целиком заполненными зонами расположены свободные зоны (рис. 1. б, в). Типичным примером таких тел являются химические элементы IV группы таблицы Менделеева: углерод в модификации алмаза, кремний, германий и серое олово, имеющее структуру алмаза. К этой же группе тел относятся многие химические соединения – оксиды металлов, нитриды, карбиды, галогениды щелочных металлов и т.д.

2.6 Эффективная масса носителей заряда.

Поле действует на электрон с силой F= . Скорость движения электрона в кристалле равна групповой:

За время dt сила F совершает работу по перемещению электрона

Дифференцируя по времени найдем ускорение

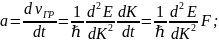
Из этой формулы следует, что под действием внешней силы F электрон в периодическом поле кристалла двигается так, как двигался бы под действием этой силы свободный электрон, если бы он обладал массой.

; -эффективная масса носителей заряда.

Эффективная масса не является массой в обычном смысле слова.

Рис. 1. Зависимость от волнового вектора энергии элек трона (а), скорости движения (б) и эффективной массы (в).