2. Обработка результатов измерения искажений

Высокая верность – важное требование для передачи дискретной информации. Термин «верность» означает защищенность от появления ошибок. Для оценки этого параметра используется вероятность ошибок по знакам (кодовым комбинациям, блокам, кадрам) или единичным элементам (символам кода). Конкретные значения допустимой вероятности ошибок зависят от назначения информации и методов ее обработки. Например, при передаче статистических данных по погрузке и выгрузке вагонов достаточно, чтобы вероятность ошибок не превышала 10^–4 – 10^–5 на знак; при передаче данных, связанных с управлением сложными технологическими процессами, – 10^–6, бухгалтерских данных по денежным расчетам – 10^–7– 10^–8, для телеграфной связи – 310^–5.

Верность можно повысить разными методами:

улучшением качественных показателей каналов связи, каналообразующей аппаратуры и оконечных устройств передачи и приема дискретной инфор-мации;

введением различного рода избыточности (например, использованием систем с обратными связями, корректирующих кодов и т. д.).

Основными причинами появления ошибок являются искажения дискретных сигналов, нарушение синхронности и синфазности работы передающих и приемных устройств. В курсовом проекте следует произвести расчет вероят-ности ошибок, обусловленных искажениями сигналов, и выбрать способы защиты, при которых будет обеспечена заданная верность передачи данных.

Искажения дискретных сигналов могут быть регулярными и случайными. К регулярным относятся искажения, обусловленные несоблюдением норм технического обслуживания аппаратуры (отклонение напряжения источников питания от номинала, регулировка входных и выходных реле с преобладанием), плавными изменениями уровня в системах тонального телеграфирования с амплитудной модуляцией, сдвигом частот в системах с частотной модуляцией, несоответствием ширины спектра канала скорости модуляции и др. Причинами искажений случайного характера являются аддитивные и мультипликативные помехи и кратковременные прерывания канала связи.

Изучение искажений можно вести двумя путями:

аналитически – на основе зависимостей между первичными характерис- тиками каналов (амплитудно- и фазочастотными характеристиками, скачками уровня, шумами и др.) и величиной искажений;

экспериментально – непосредственным измерением искажений.

Первый путь сложен и не всегда дает точные результаты вследствие

невозможности учета всех факторов, влияющих на передаваемые сигналы. На действующих каналах связи целесообразно использовать второй путь. Результаты измерения отражают не только наличие и интенсивность помех в канале, но и качество настройки аппаратуры, позволяя в ряде случаев установить причины появления искажений.

Для определения статистической структуры краевых искажений применяют анализатор искажений 1. Используя результаты измерений таким прибором, которые приведены в табл. 2, необходимо рассчитать оценки математического ожидания  и среднеквадратического отклонения :

; (1)  = (2)

где _i – среднее значение смещения значащего момента восстановления (ЗМВ), т. е. искажение для i-го интервала;

n_i – количество смещений в i-м интервале (частота смещений);

m – количество интервалов.

Результаты измерения искажений необходимо представить в виде гис-тограмм 1, с. 47. По оси абсцисс следует откладывать результаты измерений величин искажений, по оси ординат  значения где h – шаг шкалы измерителя (h = 2 %). Форма гистограммы, полученная после многочисленных исследований на проводных каналах связи с помощью анализаторов, дает основание предположить, что закон распределения смещений ЗМВ близок к нормальному, определяемому выражением:

. (3)

Нормальный закон полностью характеризуется параметрами  и . Соответствие этому закону проверяется по критерию Пирсона ² в следующем порядке.

1) Определяются теоретические значения частости смещений границ импульсов:

(4)

где h – шаг выборки (интервал смещений ЗМВ), равный двум, кроме крайних членов, где он равен 41;

Необходимо, чтобы расхождение между и не превышало 1 %.

2) Вычисляется критерий Пирсона:

(5)

причем соседние интервалы, имеющие небольшое (до пяти) количество частот n_i, объединяются в один (m₁  уточненное количество интервалов).

3) Подсчитывается количество степеней свободы:

m₂ = m₁ – b – 1, (6)

где b – число параметров теоретического распределения; b = 2, так как нормальный закон является двухпараметрическим.

4) Для значений ² и m₂ по данным справочника [3] находится вероятность выполнения критерия Р(² ). Если Р(²) ≥ 0,01, то можно утверждать, что эмпирическое распределение краевых искажений соответствует нормальному закону с параметрами  и  .

После проверки соответствия распределения искажений нормальному закону рассчитайте функцию f(δ) и нанесите ее на график гистограммы (для расчета следует взять все значения _i и обязательно значение δ = ).

Вероятность ошибки в элементе Р_э зависит от параметров распределения искажений и допустимой величины искажений :

(7)

где Ф₁ и Ф₂ – функции распределения типа 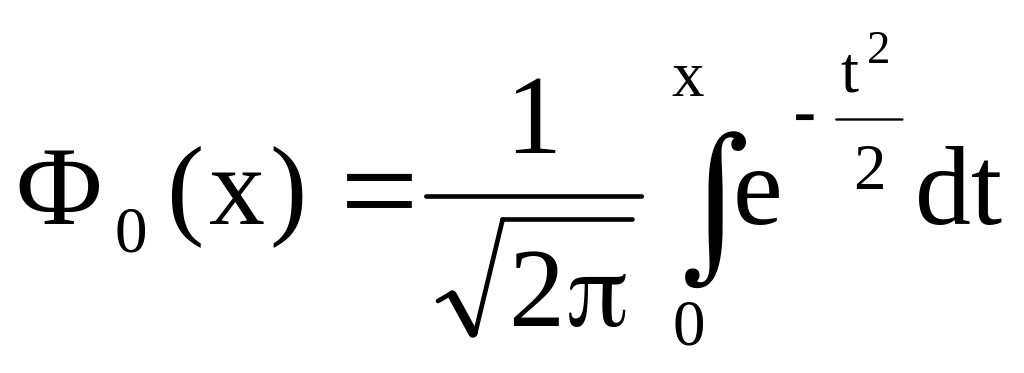нормированного центрированного нормального распределения, численные значения которых принимаются по данным справочника 3.

Следует рассчитать и построить график зависимости Р_э = f(), где  – допустимое значение искажений в пределах от 5 до 45 % (расчет вести с точ-ностью до девяти знаков после запятой).

Вероятность ошибки в комбинации из n элементов

Р_{ош к} = , (8)

где j ­– кратность ошибки, т. е. количество неправильных разрядов в комбинации (блоке);

n – общее количество разрядов; n = k – для простого кода; n = k + r – для корректирующего кода (k и r – количество информационных и проверочных разрядов соответственно);

Р₁, Р₂, …, Р_n – вероятности однократной, двукратной, … , n-кратной ошибки.

Формула (8) может быть использована для приближенных расчетов, если предположить статистическую независимость ошибок.