
ТСАУ (Часть 2)
.pdfВ. А. НЕХАЕВ, В. А. НИКОЛАЕВ, А. Н. СМАЛЕВ
ТЕОРИЯ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
ЧАСТЬ 2
ОМСК 2014
Министерство транспорта Российской Федерации Федеральное агентство железнодорожного транспорта Омский государственный университет путей сообщения
__________________________________________________________________________________
В. А. Нехаев, В. А. Николаев, А. Н. Смалев
ТЕОРИЯ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
Часть 1
Утверждено редакционно-издательским советом университета в качестве методических указаний к самостоятельной работе студентов
на практических занятиях по теории систем автоматического управления
Омск 2014
УДК 531 (075.8)
ББК 22.21я73
Г15
Теория систем автоматического управления: Методические указания к самостоятельной работе студентов на практических занятиях. Часть 2 / В. А. Нехаев, В. А. Николаев, А. Н. Смалев; Омский гос. ун-т путей сообщения.
Омск, 2014. 43 с.
Содержат теоретические сведения по классическим методам и задачам теории систем автоматического управления. Включают в себя три раздела: дифференциальные уравнения и передаточные функции, структурная схема динамической системы, частотные характеристики систем автоматического управления.
В каждом разделе приведены подробные примеры решения задач, что должно существенно помочь студентам при выполнении индивидуальных заданий, а также подготовиться к промежуточной аттестации по дисциплине.
Предназначены для студентов третьего курса механического факультета специальности «Подвижной состав железных дорог».
Библиогр.: 3 назв. Табл. 5. Рис. 16.
Рецензенты: доктор техн. наук, профессор П. Д. Балакин; доктор техн. наук, профессор Е. И. Сковородников.
_________________________
Омский гос. университет путей сообщения, 2014
ОГЛАВЛЕНИЕ |
|
Введение ...................................................................................................................... |
5 |
1. Формирование математической модели САУ в виде дифференциальных |
|
уравнений и передаточных функций........................................................................ |
6 |
1.1. Краткие сведения из теории ........................................................................... |
6 |
1.2. Примеры решения задач ................................................................................. |
7 |
2. Топологические преобразования структурной схемы САУ ............................ |
17 |
2.1. Краткие сведения из теории ......................................................................... |
17 |
2.2. Пример решения задачи ............................................................................... |
18 |
3. Построение логарифмических амплитудной и фазовой частотных харак- |
|
теристик САУ ........................................................................................................... |
28 |
3.1. Краткие сведения из теории ......................................................................... |
28 |
3.2. Пример решения задачи ............................................................................... |
29 |
Библиографический список..................................................................................... |
42 |
3
4
ВВЕДЕНИЕ
Теория систем автоматического управления изучает динамические системы, состояние которых изменяется с течением времени под действием какихлибо факторов. Наиболее изученный класс систем автоматического управления (САУ) составляют линейные непрерывные стационарные системы, описываемые системами линейных дифференциальных уравнений с постоянными коэффициентами. Подобные САУ находят самое широкое применение в технике благодаря простоте их анализа, синтеза и физической реализации.
Для составления дифференциальных уравнений динамики линейных систем могут использоваться общие теоремы динамики (в дифференциальной форме), уравнения Лагранжа 2-го рода – для описания движения механических объектов, методы контурных токов и узловых потенциалов – для описания электротехнических процессов, а также аналоги названных методов.
Важным этапом в формализации динамики систем является разбиение их на звенья (структурная декомпозиция), особенно необходимое в том случае, если система состоит из объектов различной физической природы.
Одним из основных требований, предъявляемых к САУ, является устойчивость. Понятие устойчивости динамической системы связано с ее способностью возвращаться в состояние равновесия после исчезновения внешних факторов, которые вывели ее из этого состояния. Различают устойчивость равновесия и устойчивость движения. В последнем случае под устойчивостью понимают нечувствительность системы к посторонним возмущениям, что является необходимым условием ее стабильного функционирования. Оценить устойчивость системы можно по ее частотным характеристикам. В частности, исследование логарифмических частотных характеристик обеспечивает большие возможности при синтезе систем с заданными показателями ее устойчивости и качества.
Методические указания содержат теоретические сведения по классическим методам и задачам теории систем автоматического управления и включают в себя три раздела: дифференциальные уравнения и передаточные функции, структурная схема динамической системы, частотные характеристики систем автоматического управления. В каждом разделе приведены подробные примеры решения задач, что должно существенно помочь студентам при выполнении индивидуальных заданий, а также подготовиться к промежуточной аттестации по дисциплине.
5
1. ФОРМИРОВАНИЕ МАТЕМАТИЧЕСКОЙ МОДЕЛИ САУ В ВИДЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ И ПЕРЕДАТОЧНЫХ ФУНКЦИЙ
1.1. Краткие сведения из теории
Процессы в любой динамической системе в общем случае могут быть описаны дифференциальным уравнением n-го порядка вида:
a |
d n y(t) |
a |
d n 1 y(t) |
... a |
y(t) b |
d m x(t) |
b |
d m 1x(t) |
... b x(t), (1) |
|
dtn |
dtn 1 |
dtm |
dtm 1 |
|||||||
n |
n 1 |
0 |
m |
m 1 |
0 |
где x(t) – входной сигнал (внешнее воздействие); y(t) – выходной сигнал (реакция системы);
ai, bj – коэффициенты уравнения, постоянные для линейных стационарных систем.
Для того, чтобы составить уравнения динамики процессов в электрической схеме, можно воспользоваться законами Кирхгофа. Основными элементами расчетной (принципиальной) схемы электрической цепи переменного тока (в общем случае) являются резисторы, рассеивающие электрическую энергию, катушки индуктивности, характеризующие инерционные свойства системы, и конденсаторы, способные запасать электрический заряд, а вместе с ним и потенциальную энергию.
Для формирования математической модели динамических процессов в механической системе применяют метод для энергий (уравнение Лагранжа 2-го рода) или для сил, действующих в системе на каждый ее элемент (метод Даламбера – Лагранжа, называемый общим уравнением динамики). Количество обобщенных координат, а следовательно, и уравнений в системе, определяется числом степеней свободы в рассматриваемой расчетной схеме.
Если динамика системы задана уравнением (1), то, преобразовав его по Лапласу, получим выражение в операторной форме:
a snY (s) a |
sn 1Y (s) ... a Y (s) b |
sm X (s) b |
sm 1X (s) ... b X (s), |
(2) |
||||
n |
n 1 |
0 |
m |
m 1 |
0 |
|
||
откуда можно выразить передаточную функцию в виде отношения двух полиномов:
6
W (s) |
Y (s) |
|
b sm b |
sm 1 |
... b |
|
|
||
|
m |
m 1 |
0 |
, |
(3) |
||||
X (s) |
a sn a |
sn 1 |
... a |
||||||
y/ x |
|
|
|
||||||
|
|
|
|
|
|
|
|
||
|
|
|
n |
n 1 |
|
0 |
|
|
|
где X(s) и Y(s) – изображение входного и выходного сигналов.
1.2. Примеры решения задач
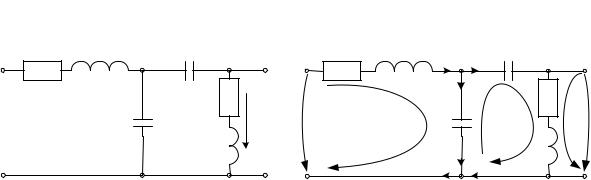
Пример 1. Определить систему дифференциальных уравнений динамики электрической системы, заданной принципиальной схемой на рис. 1; найти передаточные функции для выходных сигналов e2(t) и i2(t) по входному воздействию e1(t).
R1 |
L1 |
C2 |
A |
R1 |
L1 |
i1 |
B |
C2 |
C |
|
|
|
|
|
i2 |
||||
|
|
R2 |
|
|
|
|
i3 |
|
R2 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
e1 |
C1 |
|
e2 e1 |
I |
|
C1 |
|
II |
III e2 |
|
|
L2 |
i2 |
|
|
|
i3 |
|
L2 |
|
|
|
|
|
i1 |
i2 |
|||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||
|
|
|
F |
|
|
|
E |
|
D |
|
|
а |
|
|
|
|
б |
|
|
Рис. 1. Принципиальная схема электрической цепи: исходная (а) и
сиспользуемыми в решении обозначениями (б)
Ре ш е н и е.
Выполним некоторые построения на схеме (рис. 1, б), которые нам понадобятся в дальнейшем для решения задачи. Сначала отметим узловые точки A, B, C, D, E, F и направления токов в узле B. Согласно первому закону Кирхгофа входной ток в узел B равен сумме выходящих из него токов:
i1(t) i2 (t) i3 (t). |
(4) |
Соотношение (4) справедливо и для узла E.
Теперь обозначим три контура, чтобы воспользоваться вторым законом Кирхгофа и составить уравнения для падения напряжения вдоль каждого из контуров, пользуясь соотношениями (5) – (7) из работы [3]. При этом замкнутым является только контур II. Выберем направления обхода контуров, как показано пунктирные стрелками на рис. 1. Если направление тока совпадает с направлением обхода, то падение напряжение на элементе, через который протекает этот ток, берется со знаком «+», в противном случае – со знаком «–».
7
В контуре I падение напряжения происходит последовательно на резисторе R1, катушке L1 (через них протекает ток i1) и конденсаторе С1 (ток i3) и в сумме его значение равно входному напряжению e1 (направление всех токов совпадает с обходом контура). В контуре II (замкнутом) суммарное падение напряжения на конденсаторе C1 (ток i3 ), конденсаторе C2, резисторе R2, катушке L2 (везде ток i2) равно нулю (только ток i3 направлен против обхода контура). В контуре III подразумевается, что падение напряжения на резисторе R2 и катушке L2 равно выходному напряжению e2.
Считается, что входное напряжение e1 задано (известно). Тогда после составления уравнений для трех контуров по второму закону Кирхгофа окажется, что неизвестных четыре (три тока и выходное напряжение e2). Следовательно, к полученным трем уравнениям необходимо добавить еще одно – для токов, полученное согласно первому закону Кирхгофа. Это уравнение (4), его мы запишем третьим в системе:
|
|
|
|
|
|
|
di1 (t) |
1 |
|
|||||
e1 |
(t) R1i1 (t) L1 |
|
|
|
|
|
|
|
||||||
|
|
dt |
|
C |
||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
1 |
i3 |
(t)dt |
1 |
i2 (t)dt |
|||||||
0 |
|
|
|
|||||||||||
|
|
|
||||||||||||
|
|
|
C1 |
|
|
|
|
C2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i1 |
(t) i2 (t) i3 (t); |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
di2 (t) |
|
|
|
|
||||
|
e (t) R i (t) L |
|
. |
|
|
|||||||||
|
|
|
|
|
|
|
|
|||||||
2 |
|
|
2 2 |
2 |
|
|
dt |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i3 (t)dt; |
|
|
|
||
R2i2 |
(t) L2 |
di2 |
(t) |
; |
|
dt |
|||||
|
|
(5) |
|||
|
|
|
|
||
Итак, составлена система уравнений, описывающих динамику электрической системы (они являются дифференциально-интегральными). Очевидно, что последнее уравнение системы (5) является единственным, которое содержит сигнал e2, который связан непосредственно с током i2. Следовательно, первые три уравнения могут быть решены без рассмотрения последнего, однако оно нам необходимо для определения именно сигнала e2.
Чтобы найти передаточные функции для сигналов e2 и i2, потребуется преобразовать левые и правые части уравнений системы (5) по Лапласу, пользуясь его свойствами и соотношениями (8) – (10) из работы [3], а затем определить изображения указанных сигналов. После выполненных преобразований система в операторной форме примет вид:
8

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
||
E1 (s) R1I1 (s) L1sI1(s) |
|
|
I3 (s); |
|
|
|||||||||||||||||
C1s |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
1 |
|
|
I3 (s) |
|
|
|
1 |
|
(s) R2 I2 |
(s) L2sI2 |
|
|
||||||||
0 |
|
|
|
|
|
|
|
|
I2 |
(s); |
|
|||||||||||
C1s |
C2s |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
(6) |
|||||||||
I (s) I |
|
|
(s) I |
(s); |
|
|
|
|
|
|
|
|
|
|||||||||
1 |
|
|
2 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R2 I2 (s) L2 I2 (s). |
|
|
|
|
|
|
|
|||||||||||||
E2 (s) |
|
|
|
|
|
|
|
|||||||||||||||
Умножим первое уравнение на C1s, а второе – на C1C2s и, где это возмож- |
||||||||||||||||||||||
но, вынесем токи за скобки как общие множители: |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C1sE1 (s) |
C1L1s |
2 |
|
C1R1s I1 |
(s) |
I3 (s); |
|
|
|||||||||||||
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C2 I3 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
0 |
(s) C1L2C2s C1R2C2s C1 I2 (s); |
|
||||||||||||||||||||
|
|
I2 (s) I3 (s); |
|
|
|
|
|
|
|
|
(7) |
|||||||||||
I1 |
(s) |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E (s) L s R I |
2 |
(s). |
|
|
|
|
|
|
|
|
||||||||||||
|
2 |
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
После применения преобразования необходимо решить систему линейных алгебраических уравнений (СЛАУ) относительно изображений искомых сигналов. Сначала решим первые три уравнения и определим ток I2(s). Затем, подставив полученное выражение для тока I2(s) в четвертое уравнение, найдем напряжение E2(s).
Будем решать систему методом Крамера. Для этого в первую очередь перенесем неизвестные токи в левую часть уравнений системы, а известное входное напряжение – в правую:
|
|
|
|
|
|
|
|
|
|
C1L1s |
2 |
C1R1s I1 (s) I3 |
(s) |
C1sE1(s); |
|
||||
|
|
||||||||
|
|
|
|
|
2 |
|
|
(s) C2 I3 (s) 0; |
(8) |
|
|
|
|
|
|
||||
C1L2C2s |
|
C1R2C2s C1 I2 |
|||||||
|
|
|
I2 (s) I3 (s) 0. |
|
|
|
|||
I1 |
(s) |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
После этого введем вектор неизвестных токов I (s) следующим образом:
I1 (s)
I (s) I2 (s) . (9)I3 (s)
9
