Вариант № 52406

1. B 8 . Н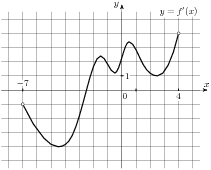 а ри­сун­ке изоб­ра­жен гра­фик про­из­вод­ной функ­ции , опре­де­лен­ной на ин­тер­ва­ле (−7; 4). Най­ди­те про­ме­жут­ки убы­ва­ния функ­ции .

В от­ве­те ука­жи­те сумму целых точек, вхо­дя­щих в эти про­ме­жут­ки.

По­яс­не­ние.

Про­ме­жут­ки убы­ва­ния функ­ции f(x) со­от­вет­ству­ют про­ме­жут­кам, на ко­то­рых про­из­вод­ная функ­ции от­ри­ца­тель­на, то есть ин­тер­ва­лу (−7; −2,5). Дан­ный ин­тер­вал со­дер­жит сле­ду­ю­щие целые точки: −6, −5, −4, −3, сумма ко­то­рых равна −18.

 

Ответ: −18.

Ответ: -18

2. B 8 . 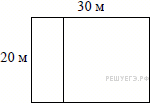Дач­ный уча­сток имеет форму пря­мо­уголь­ни­ка со сто­ро­на­ми 20 мет­ров и 30 мет­ров. Хо­зя­ин пла­ни­ру­ет об­не­сти его за­бо­ром и раз­де­лить таким же за­бо­ром на две части, одна из ко­то­рых имеет форму квад­ра­та. Най­ди­те общую длину за­бо­ра в мет­рах.

По­яс­не­ние.

Длина за­бо­ра равна сумме пе­ри­мет­ра и ши­ри­ны. Най­дем пе­ри­метр участ­ка 30+30+20+20=100 м.

Длина за­бо­ра 100+20=120 м.

 

Ответ: 120.

Ответ: 120

3. B 8 . На ри­сун­ке изоб­ражён гра­фик функ­ции и одной из пер­во­об­раз­ных не­ко­то­рой функ­ции , опре­делённой на ин­тер­ва­ле Поль­зу­ясь ри­сун­ком, опре­де­ли­те ко­ли­че­ство ре­ше­ний урав­не­ния на от­рез­ке

По­яс­не­ние.

По опре­де­ле­нию пер­во­об­раз­ной на ин­тер­ва­ле (−2; 4) спра­вед­ли­во ра­вен­ство

 

 

Сле­до­ва­тель­но, ре­ше­ни­я­ми урав­не­ния f(x) = 0 яв­ля­ют­ся точки экс­тре­му­мов изоб­ра­жен­ной на ри­сун­ке функ­ции F(x) Это точки −1,5; −1,2; −0,6; −0,2; 0,2; 0,5; 1,2; 1,8; 2,5; 2,8; 3,2. Из них на от­рез­ке [−1; 3] лежат 8 точек. Таким об­ра­зом, на от­рез­ке [−1; 3] урав­не­ние f(x) = 0 имеет 8 ре­ше­ний.

 

Ответ: 8.

Ответ: 8

4. B 8 . На ри­сун­ке изоб­ра­жен гра­фик про­из­вод­ной функ­ции f(x), опре­де­лен­ной на ин­тер­ва­ле (−10; 2). Най­ди­те ко­ли­че­ство точек, в ко­то­рых ка­са­тель­ная к гра­фи­ку функ­ции f(x) па­рал­лель­на пря­мой y = −2x − 11 или сов­па­да­ет с ней.

 

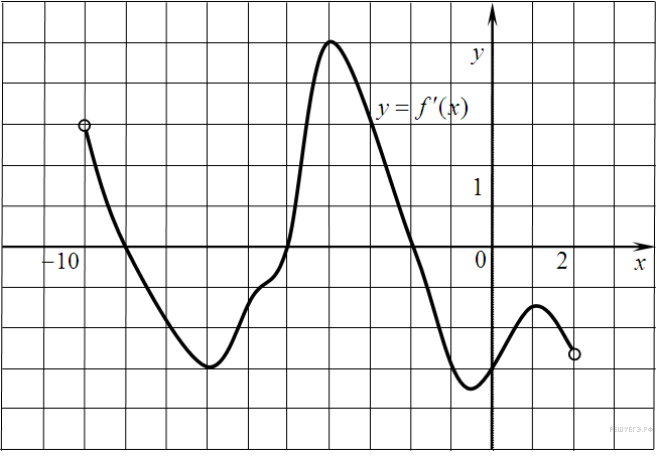
По­яс­не­ние.

Зна­че­ние про­из­вод­ной в точке ка­са­ния равно уг­ло­во­му ко­эф­фи­ци­ен­ту ка­са­тель­ной. По­сколь­ку ка­са­тель­ная па­рал­лель­на пря­мой y = −2x − 11 или сов­па­да­ет с ней, их уг­ло­вые ко­эф­фи­ци­ен­ты равны –2. Най­дем ко­ли­че­ство точек, в ко­то­рых y'(x₀) = −2, это со­от­вет­ству­ет ко­ли­че­ству точек пе­ре­се­че­ния гра­фи­ка про­из­вод­ной с пря­мой y = −2. На дан­ном ин­тер­ва­ле таких точек 5.

 

Ответ: 5.

Ответ: 5

5. B 8 . 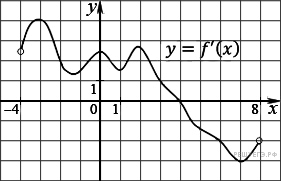На ри­сун­ке изоб­ра­жен гра­фик про­из­вод­ной функ­ции f(x), опре­де­лен­ной на ин­тер­ва­ле (−4; 8). Най­ди­те точку экс­тре­му­ма функ­ции f(x) на от­рез­ке [−2; 6].

По­яс­не­ние.

Если про­из­вод­ная в не­ко­то­рой точке равна нулю, а в ее окрест­но­сти ме­ня­ет знак, то это точка экс­тре­му­ма. На от­рез­ке [–2; 6] гра­фик про­из­вод­ной пе­ре­се­ка­ет ось абс­цисс, про­из­вод­ная ме­ня­ет знак с плюса на минус. Сле­до­ва­тель­но, точка 4 яв­ля­ет­ся точ­кой экс­тре­му­ма.

 

Ответ: 4.

Ответ: 4

6. B 8 . На ри­сун­ке изоб­ражён гра­фик про­из­вод­ной функ­ции на оси абс­цисс от­ме­че­ны шесть точек: , , , , . Сколь­ко из этих точек лежит на про­ме­жут­ках воз­рас­та­ния функ­ции

 

По­яс­не­ние.

По­ло­жи­тель­ным зна­че­ни­ям про­из­вод­ной со­от­вет­ству­ют ин­тер­ва­лы, на ко­то­рых функ­ция воз­рас­та­ет. В этих ин­тер­ва­лах лежат точки Таких точек 2.

 

Ответ: 2.

 

---------

Дуб­ли­ру­ет за­да­ние 317745.

Ответ: 2

7. B 8 . 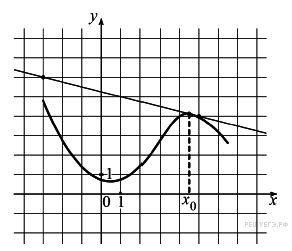На ри­сун­ке изоб­ра­же­ны гра­фик функ­ции y = f(x) и ка­са­тель­ная к нему в точке с абс­цис­сой x₀. Най­ди­те зна­че­ние про­из­вод­ной функ­ции f(x) в точке x₀.

По­яс­не­ние.

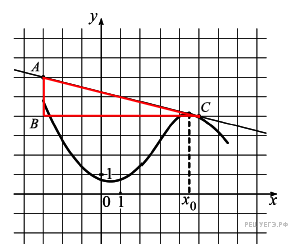Зна­че­ние про­из­вод­ной в точке ка­са­ния равно уг­ло­во­му ко­эф­фи­ци­ен­ту ка­са­тель­ной, ко­то­рый в свою оче­редь равен тан­ген­су угла на­кло­на дан­ной ка­са­тель­ной к оси абс­цисс. По­стро­им тре­уголь­ник с вер­ши­на­ми в точ­ках A (−3; 6), B (−3; 4), C (5; 4). Угол на­кло­на ка­са­тель­ной к оси абс­цисс будет равен углу, смеж­но­му с углом ACB:

 

.

 

Ответ: −0,25.

Ответ: -0,25

8. B 8 . Уча­сток земли для стро­и­тель­ства са­на­то­рия имеет форму пря­мо­уголь­ни­ка, сто­ро­ны ко­то­ро­го равны 900 м и 400 м. Одна из бóльших сто­рон участ­ка идёт вдоль моря, а три осталь­ные сто­ро­ны нужно от­го­ро­дить за­бо­ром. Най­ди­те длину этого за­бо­ра. Ответ дайте в мет­рах.

По­яс­не­ние.

Длина за­бо­ра равна сумме длин двух ко­рот­ких сто­рон и одной длин­ной сто­ро­ны: 400 + 400 + 900 = 1700 мет­ров.

 

Ответ: 1700.

Ответ: 1700

9. B 8 . Ма­те­ри­аль­ная точка дви­жет­ся пря­мо­ли­ней­но по за­ко­ну (где — рас­сто­я­ние от точки от­сче­та в мет­рах,  — время в се­кун­дах, из­ме­рен­ное с на­ча­ла дви­же­ния). Най­ди­те ее ско­рость (в м/с) в мо­мент вре­ме­ни

По­яс­не­ние.

Най­дем закон из­ме­не­ния ско­ро­сти:

 

При имеем:

 

Ответ: 35.

Ответ: 35

10. B 8 .

Ма­те­ри­аль­ная точка дви­жет­ся пря­мо­ли­ней­но по за­ко­ну (где x —рас­сто­я­ние от точки от­сче­та в мет­рах, t — время в се­кун­дах, из­ме­рен­ное с на­ча­ла дви­же­ния). Най­ди­те ее ско­рость (в м/с) в мо­мент вре­ме­ни t = 3 с.