1.8 Количественная мера информации

При введении количественной меры информации (Норберт Винер и Клод Шеннон) было принято смысловое содержание сообщений (семантику) не учитывать, а ограничиваться только формальными признаками, важными с точки зрения передачи сообщений по каналам связи. В итоге учитывается только число N сообщений, подлежащих передаче, и вероятность Р(xi) поступления их на вход канала. Всю совокупность сообщений представляют в виде некоторой системы Х c состояниями xi

X= (х1 х2 … хN )

р (х1) р (х2) p (хN) ,

N

 p (xi) = 1, (1.1)

i=1

где xi - отдельные сообщения (или их типы, классы), р (xi) - априорные вероятности появления сообщений xi.

В результате передачи сообщения xi по каналу связи будет получено сообщение yј. Оно может с некоторой вероятностью быть похоже на любое из (х1, х2, … хN ) сообщений. В том числе оно может быть похоже на переданное сообщение xi. Апостериорная (послеопытная) вероятность присутствия xi в yј равна р (xi / yј).

В основу меры количества информации положены изменения вероятностей появления сообщений от априорного значения p (xi) на входе канала к апостериорному значению р (xi / yј) на выходе канала, связанные с искажениями информации в канале. Сравнивая вероятности p (xi) и р (xi / yј) можно установит меру количества информации, переданной через данный канал. Удобной мерой оказался логарифм отношения апостериорной вероятности к априорной.

Количество информации, содержащееся в событии yј относительно события xi определяется по формуле

I( xi ; yј ) = log р (xi / yј) / p (xi) (1.2)

Основанием логарифма могут быть: 2, e или 10. В зависимости от основания меняются единицы измерения количества информации (бит – дв. ед.; нит – нат. ед.;Хартли – дес. ед.)

Свойства количества информации I (xi;yi)

1. Свойство симметрии.

Информация, содержащаяся в yј относительно xi, равна информации, содержащейся в xi относительно yј. Это становится очевидным, если числитель и знаменатель в (1.2) умножить на p(yј) и произвести преобразования:

I( xi , yј ) = log р (xi /yј)ּp (yј) / p (xi)ּp (yј) =

= log р (xi ,yј) / p (xi)ּp (yј) = I( xi ; yј ),

поскольку р (xi , yј) = p (yј)ּp(xi / yj) = p (xi)ּp(yj / xi) - вероятность совместного появления yј и xi.

В результате указанного свойства величину I (xi ; yј) называют количеством взаимной информации между xi и yј.

2. Свойство аддитивности

Информация, содержащаяся в паре символов yј, zk относительно xi, равна сумме информации, содержащейся в уј относительно хi и информации, содержащейся в zk относительно xi при условии, что значение yј известно

I( xi ; yј ; zk) = I( xi ; yј) + I( xi ; zk / yј ). (1.3)

Количество собственной информации в xi определяется из (1.2) при p(xi / yj) = 1

I(xi) = - log р (xi). (1.4)

Эта величина определяет количество информации, необходимое для однозначного определения xi на выходе канала.

С учетом введенного понятия (1.4) можно преобразовать выражение (1.2) к виду

I( xi ; yј) = I(xi) - I( xi / yј),

где I (xi / yј) = - log p (xi / yј) - условная собственная информация.

Среднее количество взаимной информации получается путем усреднения (1.2) по всем i и ј:

N M

I( Х ; У) = ∑ ∑ p (xi , yј) ּlog p (xi / yј) / p (xi)

i=1 ј=1

Энтропия

Она определяет меру неопределенности всего множества сообщений на входе канала и вычисляется как среднее количество собственной информации во всех сообщениях:

I( Х ) = - ∑ p (xi) ּlog p (xi) = H(X).

Свойства энтропии:

Энтропия Н(Х) неотрицательна.

Энтропия Н(Х) ≤ log N.

Величина log N = D называется информационной пропускной способностью алфавита (информационной емкостью алфавита).

Если N = 2, то р(х1) = р, р(х2) = 1-р

Н(Х) = - р log p - (1-p) log (1-p).

Максимум Н(Х) =log 2=1 – емкость двоичного алфавита равна 1 бит.

З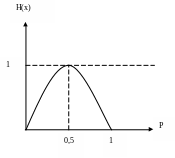 ависимость H(X) от величины р:

Рис. 1.1.

Для объединенных ансамблей

N M

H( X, Y) = - ∑ ∑ p (xi , yј) ּlog p (xi , yј). (1.6)

i=1 ј=1

Частная условная энтропия

M

H( Y/xi) = - ∑ p ( yј /xi ) ּlog p ( yј / xi ). (1.7)

ј=1

Среднее значение частных условных энтропий называется условной энтропией

N

H( Y / X ) = - ∑ p ( xi ) ּ H( Y/xi). (1.8)

i=1

Она характеризует неопределенность исхода событий у при известных событиях х.

Если учесть, что математическое ожидание есть результат усреднения по всем состояниям, то выражения (1.5), (1.6) и (1.8) можно записать в виде

N

Н(Х) = - ∑ p ( xi ) ּlog p ( xi ),

i=1

Н(Y/X) = M [ - log p (Y / X)],

Н(X,Y) = M [- log p (xi , yј)],

где М – математическое ожидание. Из теории вероятности известно, что p (x, y) = p (x) p (у/х) = р(у) р(х/у).

После логарифмирования и применения операции поиска математического ожидания получаем соотношения:

Н(Х,У) = Н(Х) + Н(У/Х),

Н(Х,У) = Н(Х) + Н(Х/У). (1.9)

В другой форме (1.9) имеет вид

Н(Х) – Н(Х/У) = Н(У) – Н(У/Х). (1.10)

Левую часть (1.10) можно интерпретировать как среднее количество информации I(Х,У), доставленное в пункт приема, равно среднему количеству переданной информации Н(Х) минус среднее количество информации Н(Х/У), потерянное вследствие действия шумов.

Правая часть (1.10) содержит энтропию шума Н(У/Х) при известном сигнале Х. Обе части равенства (1.10) одинаково пригодны для определения среднего количества переданной по каналу информации.

Энтропия систем с непрерывным множеством состояний вычисляется по правилам анализа дискретных систем с предварительным квантованием плотности вероятности w(x) с шагом ∆х.

Тогда число состояний в системе будет равно

N = ( х max - x min ) / ∆х,

а вероятности состояний р (xi) = w(x) ∆х.

Используя известные формулы данного раздела, можем получить энтропию

N

Н ∆х (х) = - ∑ ω( xi ) ∆х ּlog {ω( xi ) ∆х }.

i=1

После преобразований и устремления ∆х к нулю получаем

Н ∆х (Х) = Н* (Х) – log ∆х. (1.11)

Величина Н*(Х) называется приведенной энтропией. Она равна

∞

Н* (Х) = -∫ ω(x) log ω(x) dx. (1.12)