7. Анализ качества объектов ис коллективного пользования

7.1. Объекты коллективного использования в структуре ис

В структуре ИС много компонент, которые используются большим числом абонентов коллективно (каналы связи, узлы распределения информации, системы хранения и обработки информации).

Устройства коллективного использования различны по своему строению, функциям, технологии обслуживания заказов. Эти их особенности подробно изучаются в специальных курсах. Здесь мы отвлекаемся от конкретной технологии обслуживания, а будем учитывать только дополнительные временные и точностные потери, связанные с организацией обслуживания абонентов.

Проблема сложности анализа таких систем обусловлена случайным характером потока заявок на обслуживание и случайным характером длительности обслуживания. В связи с чем процесс работы системы протекает нерегулярно: временами приборы обслуживания простаивают, временами образуются очереди на обслуживание. Необходимо заботиться как об уменьшении очередей, так и об исключении непроизводительных простоев приборов обслуживания.

Основоположником работ по количественному анализу систем коллективного использования в сфере информационного обслуживания является датский ученый А.К. Эрланг (1878-1929). Дальнейшее развитие этих работ было в трудах советского математика А.Я. Хинчина (1894 - 1959), который назвал этот раздел прикладной математики теорией массового обслуживания.

Математическая модель систем массового обслуживания (СМО) включает три основных элемента:

а) поток событий;

б) схему распределения ресурсов;

в) дисциплину обслуживания.

Событиями в СМО являются причины перехода системы из одного состояния в другое. Причинами перехода могут быть: поступление заявки на обслуживание, завершение этапа обслуживания, постановка заявки в очередь, покидание ею очереди.

Эти события следуют одно за другим, образуя поток событий, который характеризуется своими параметрами. Нас будут интересовать такие параметры: длительность промежутков между соседними событиями или число заявок на заданном интервале времени. Эти параметры носят случайный характер.

Схема распределения ресурсов определяет порядок доступа заявок к обслуживающим приборам. Возможны варианты построения, когда к каждому обслуживающему прибору организуется своя очередь. Более выгодной может оказаться общая очередь ко всем ресурсам обслуживания; возможны и промежуточные варианты.

Дисциплина обслуживания характеризует особенности взаимодействия потока вызовов с системой обслуживания. Она учитывает:

способы обслуживания заявок (с потерями, с ожиданием, комбинированное обслуживание);

порядок обслуживания заявок (в порядке очередности поступления, в случайном порядке и т.д.);

наличие преимуществ(приоритетов) в обслуживании некоторых категорий заявок;

наличие ограничений при обслуживании (по длительности ожидания, длительности обслуживания, числу ожидающих заявок и пр.).

Обобщенная математическая модель СМО представлена на рис. 7.1.

.

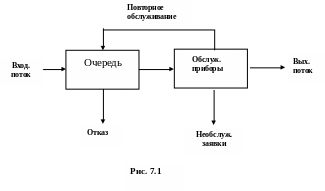
В научной литературе для компактной записи математических моделей СМО пользуются условными обозначениями из последовательности символов, разделенных наклонной чертой (например, М/М/m). Первый символ обозначает функцию распределения промежутков между заявками во входном потоке ( М- показательное, Е – эрланговское, D – равномерной плотности, G- произвольное распределение). Второй символ обозначает функцию распределения длительности обслуживания ( что эквивалентно распределению промежутков между событиями в выходном потоке). Значения букв те же, что и в первом случае.

Третий символ указывает на число приборов обслуживания.

Процесс функционирования СМО представляет собой случайный процесс: в случайные моменты времени система скачкообразно переходит из одного состояния в другое (меняется число занятых каналов, число заявок, длина очереди и т.д.) Исследование этих процессов связано с анализом потоков событий.