5.5. Корреляционный метод обнаружения
Принятие решения не по одному значению какой-то величины, а по большому числу N значений позволяет получить больший положительный эффект, если различные отсчеты взаимно независимы. Для выполнения этого условия отсчеты должны отстоять друг от друга не менее, чем на - интервал корреляции помехи. Для помехи типа «белого шума» –> 0. В этом случае
=
.
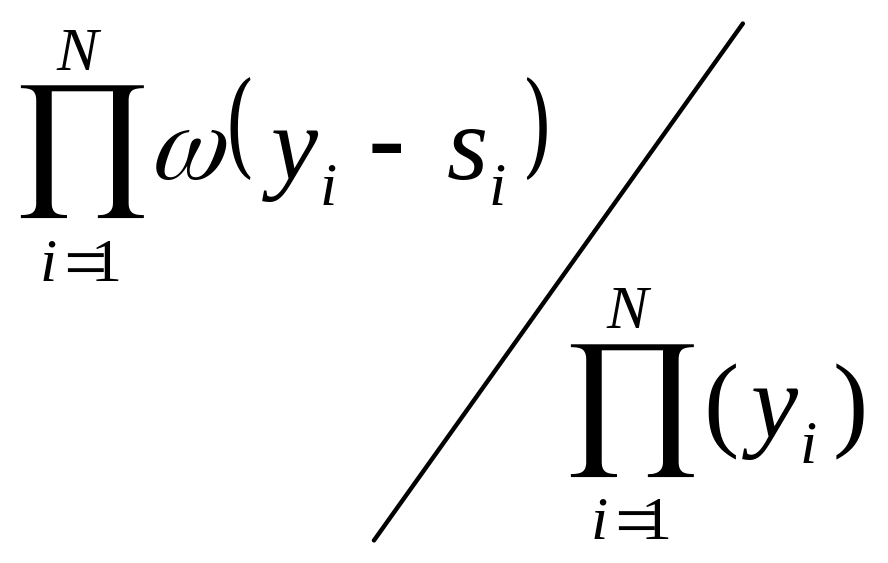(5.26)
Для нормальных случайных процессов с нулевым средним и дисперсией
=
.
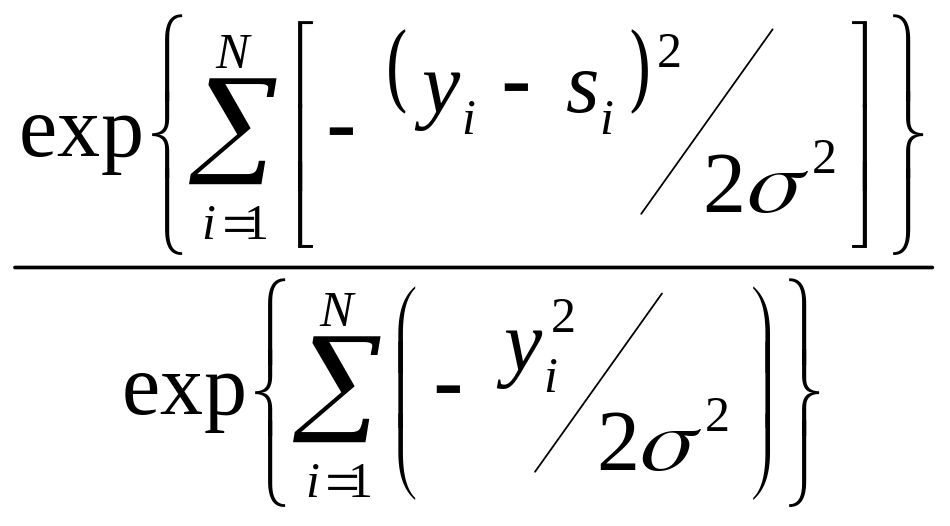(5.27)
Преобразования (5.27) сводятся к
.
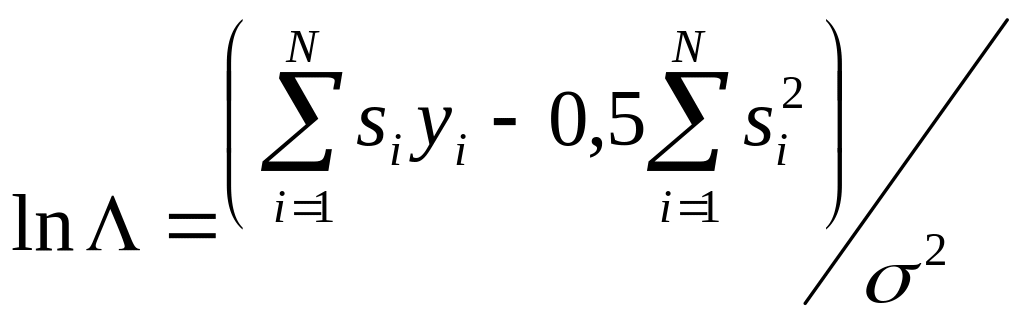(5.28)
Правило обработки удобнее представить в виде
,
(5.29)
из
которого следует, что при обработке
необходимо определить величину
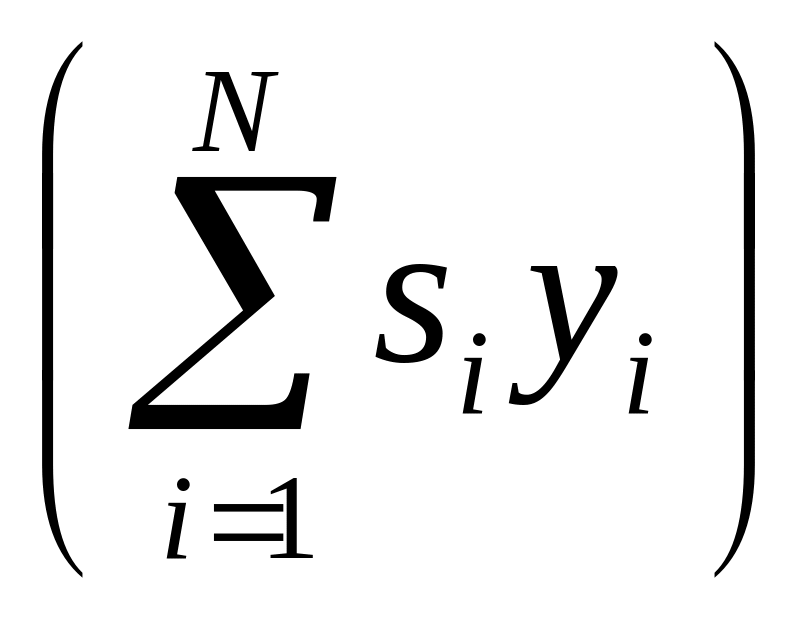и сравнить ее с порогом, равным
,
(5.30)
который получается из (5.29) при =п.
При (ay)N > (ay)пргN выдается решение «Да». Если выборка берется на интервале [0 – t], а отсчеты в ней берутся через –> 0, то суммы в (5.29) превращаются в интегралы, а величина - в спектральную плотность мощности. Поэтому имеем
><
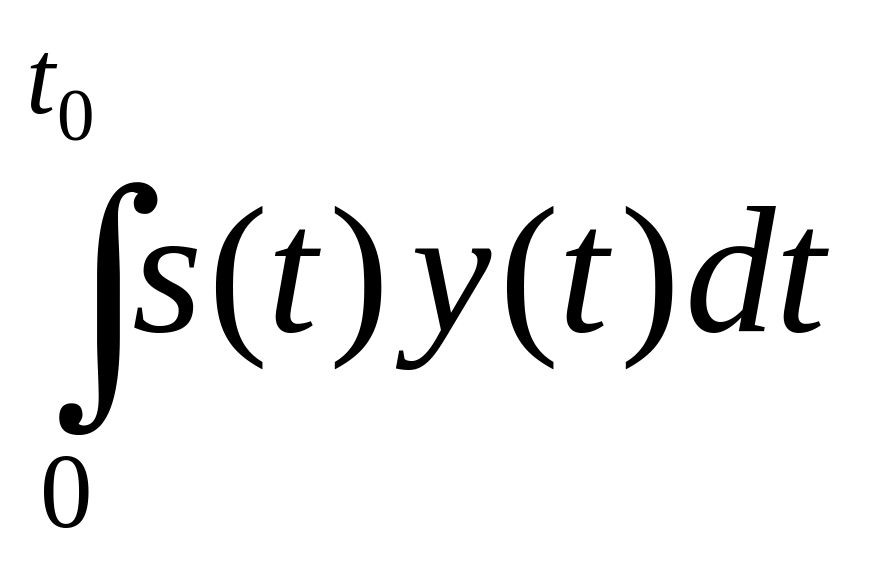ln
,
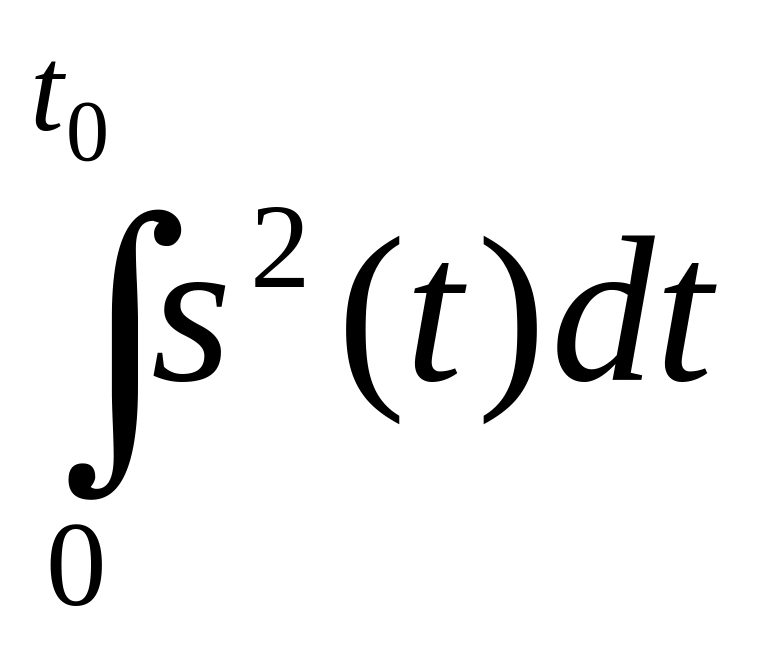(5.31)
Процедура принятия решения, предписываемая (5.31), состоит в перемножении реализации y(t) на ожидаемый сигнал s(t), интегрировании полученного произведения в пределах от нуля до t0 и сравнении результата с порогом.
Функциональная схема обнаружителя, работающего на основе корреляционного метода, показана на рис. 5.2, где П – перемножитель, И – интегратор, ПУ – пороговое устройство.
Да
П
И
ПУ
y(t)
Нет
s(t)
Рис.5.2
Интеграл является мерой взаимной корреляции между реализацией y(t) и полезным сигналом s(t). Поэтому его называют корреляционным интегралом, а описанную выше процедуру обнаружения – корреляционным методом.
Для определения вероятностных характеристик обнаружения следует учесть, что в отсутствии полезного сигнала y(t) = (t) и
-
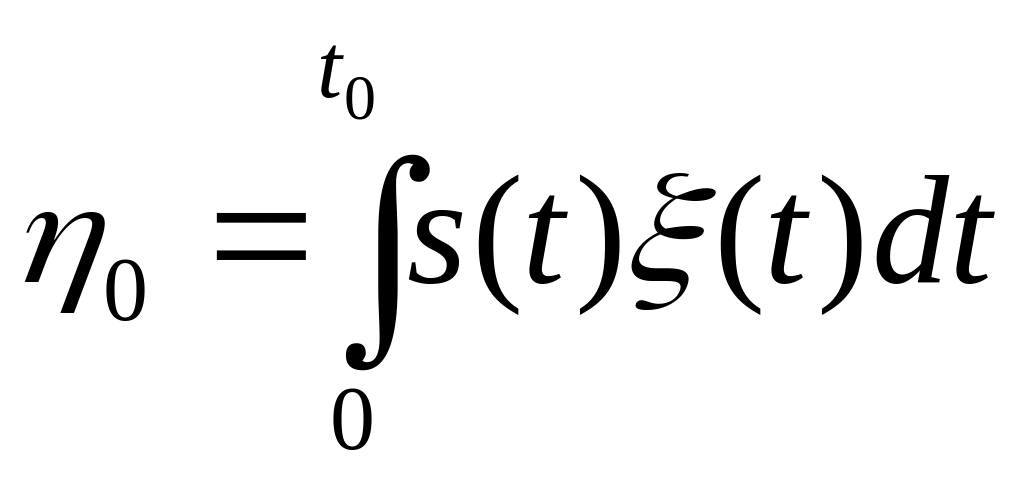случайная величина,
а при наличии сигнала y(t) = s(t) + (t) и
.
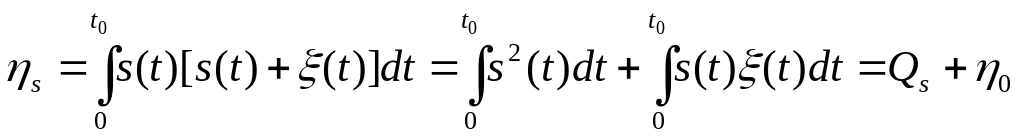(5.32)
Условные вероятности Pлт и Pпрп определяются по той же методике, что и в случае однократного отсчета с предварительным уточнением закона распределения, математического ожидания и дисперсии случайных величин и s .
5.6. Синтез приемников непрерывных сигналов
Эта задача относится к классу выделения сигналов на фоне помех (или воспроизведения сообщений, задачей фильтрации). Впервые она сформулирована и решена Н. Винером в 1941 г.
Пусть на вход приемника поступает сигнал с помехой
y(t) = s(t) + (t).
Приемник характеризуется передаточной функцией K(i), которую необходимо определить. Этапы поиска сводятся к следующему.
K(i)
y(t)
(t)
Рис. 5.3
Сигнал на выходе приемника
,
(5.33)
,
где g(импульсная переходная функция.
Ошибка в воспроизведении сигнала равна
(t) = s(t) + (t).
Задача формулируется так, чтобы найти передаточную функцию K(i) приемника, обеспечивающую минимальное значение среднего квадрата ошибки
.
(5.34)
После подстановки в (5.34) известных и искомых величин задача сводится к интегральному уравнению, решить которое можно методами вариационного исчисления. Решение, полученное Н. Винером, имело вид
,
(5.35)
где S(), N() – энергетические спектры сигнала и помехи.
Дальнейшие поиски привели к уточнению критерия оптимальности и несколько другому решению. Стали искать фильтр, обеспечивающий максимум отношения сигнала к шуму на выходе фильтра. Оказалось, что такое условие обеспечивает фильтр (приемник) с передаточной функцией
,
(5.36)
где a, t0 – постоянные значения,
S*(i) – спектр, сопряженный со спектром сигнала.
Другими словами, передаточная функция приемника должна быть согласована со спектром сигнала. Отсюда пошел термин согласованной фильтрации.
Получаемое на выходе приемника отношение сигнала к шуму равно
,
где
- энергия сигнала на входе приемника,
N0 – энергетический спектр помех.
Заметим, что сигнал на выходе согласованного фильтра совпадает по форме с автокорреляционной функцией входного сигнала, так как
,
а для согласованного фильтра g(t)= A0sвх(t-). Поэтому
,
где =t - t0.
Это означает, что приемник можно строить по правилам вычисления взаимно корреляционной функции входного сигнала с ожидаемым. На рис. 5.4 показана корреляционная функция отрезка гармонического колебания.
Т
s(t)
t
K()
T0=T
Рис. 5.4