3.7 Математические модели преобразующих элементов

Информационные процессы, реализуемые в ИС, весьма разнообразны. Их прикладная направленность вообще необъятна. Однако внесение некоторой доли абстракции и обобщения понятий число видов преобразований информации можно существенно уменьшить. Наиболее характерные для ИС преобразования:

• перенос информации в пространстве (передача - прием);

• перенос информации во времени (хранение);

• определение влияния информации на реальные объекты, процессы и явления (обработка содержательная);

• упорядочивание объемов информации (обработка формальная);

• изменение носителей и формы представления информации (отображение, документирование).

Анализ любого из перечисленных видов преобразований осуществляется с помощью моделей поведения макроуровня и микроуровня. МП макроуровня учитывают интегральные характеристики преобразований. Схемы таких моделей содержат обобщенный преобразующий элемент ПЭ, на который поступает информация и преобразуется в выходную информацию в условиях действия помехи (рис. 3.3)

Помеха

ПЭ

Рис. 3.3

Цель любых преобразований сводится к снижению неопределенности знаний у получателя информации относительно интересующей его ситуации. Например, относительно состояния или поведения управляемого объекта, эффективности принимаемых решений, глубины познания реального мира, отношения некоторых субъектов к определенным событиям и т.п. Количественная оценка результатов преобразований может быть получена на базе теории информации. Однако, без детального анализа технологии преобразований и характеристик действующих помех количественные оценки получить сложно из-за нехватки априорных сведений.

Модели микроуровней предполагают раскрытие всех этапов преобразования и всех каналов взаимодействия ПЭ с внешней средой. При этом преобразующий элемент ПЭ превращается в цепь последовательно соединенных , j =1,…,m, или в сеть определенной структуры из . Получается распределенная в пространстве система преобразующих элементов, к анализу которой необходимо привлекать не только ММ , но и дисциплины обслуживания в сети по методам теории систем массового обслуживания.

Наиболее характерные для ИС частные преобразующие элементы исследуются с помощью математических моделей: источников информации, сигналов, помех, кодеров и декодеров, модуляторов и демодуляторов, табло и экранов, специализированных алгоритмов обработки сигналов, которые строятся на базе детерминированных или вероятностных математических структур.

Последующий детальный анализ математических моделей частных целесообразно проводить не в порядке следования их в заданных цепочках преобразования (поскольку они сильно различаются как составом , так и очередностью следования), а в зависимости от используемого математического аппарата.

4. Математическое описание источников информации, сигналов и помех

4.1. Математические модели источников информации и сообщений

Источники информации имеют различную физическую природу, отличаются по виду формируемых сообщений, энергетической активности, вероятностным характеристикам. Для анализа интерес представляют не только характеристики определенных сообщений, но и потоки сообщений, как специфический случайный процесс. В ИС информация с носителей различной физической природы (голос, изображение, символы на бумаге, ленте, вибрации и т.п.) преобразуются к универсальному виду и фиксируются на универсальных носителях.

В качестве универсального носителя используется электрический сигнал(или материалы, обладающие электромагнитными свойствами, позволяющие просто снимать с них информацию в виде электрических сигналов). Электрические сигналы являются переносчиками информации, а материалы – носители информации выполняют функции хранения ее.

Определение 1. Сигналом называется изменяющаяся физическая величина, являющаяся переносчиком информации.

Преобразование признаков любой физической природы в электрический сигнал можно рассмотреть на примере работы микрофонной цепи телефонного аппарата (Рис. 4.1.).

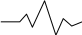U(t)

 М Z_н

t

Рис. 4.1. Рис. 4.2.

Звуковая энергия  говорящего в виде переменного давления с(t) воздействует на микрофон, содержащий внутри угольный порошок. Из-за этого меняется электрического сопротивление микрофона и, как следствие, ток U(t) повторяет звуковые колебания с(t).

Подобные преобразования могут осуществляться с использованием цепи переменного тока путем воздействия на индуктивность или емкость колебательного контура, в результате чего параметры колебательного процесса преобразуют закономерности воздействующего процесса.

В ряде датчиков улавливается оптическое (тепловое, инфракрасное) излучение, которое переносится в пространстве с помощью оптики, а затем преобразуется в электрические сигналы. В таких датчиках могут быть объединены механическая, оптическая и электронная части, а также согласующие и синхронизирующие устройства.

Если исходное сообщение представляло собой некоторую функцию с(t), то электрический сигнал

,

где F_c[c(t)] – оператор преобразования, должен повторять закон изменения с(t) в изменениях своего информационного параметра, которым на этом этапе преобразования является чаще всего величина мгновенного значения электрического тока(или напряжения). Сигнал U(t) называют «видеосигналом» из-за наличия в нем постоянной составляющей. На практике добиваются практически абсолютного сходства функций с(t) и U(t) при любой сложности их (или с точностью до масштабного множителя). Поэтому их математические модели одинаковы.

С целью упрощения анализа сигналы с(t) произвольной сложности представляют в виде суммы элементарных колебаний (t), называемых базисными функциями,

, (4.1)

где с_к – коэффициенты.

В качестве базисных функций могут использоваться многие известные системы функций(Фурье, Бесселя, Лежандра, Чебышева, Уолша и д.р.).

В технике связи используется в основном преобразование Фурье, в которых базисными являются гармонические колебания, и разложения Котельникова, в которых базисными являются функции вида sinx/x.

Преобразования Фурье позволяют перевести сообщения произвольной формы в совокупность элементарных гармонических колебаний. При этом анализ преобразований сигнала сводится к анализу изменений параметров гармонических колебаний (как элементарных «кирпичиков» сложного объекта).

Наиболее известны гармонические ряды Фурье:

, (4.2)

где =2/Т, Т- период.

Для непериодических функций Фурье установил соответствие между временными и спектральными характеристиками:

, (4.3)

где s(t)- временная функция, S(iw)- спектральная плотность.

П ару преобразований (4.3.) кратко обозначают в виде: S(iw) s(t).

Можно показать, что

.

- действительная часть спектральной плотности. - мнимая часть спектральной плотности.

- амплитудная характеристика спектральной плотности (АЧХ)- характеризует распределение по частотному спектру амплитуд гармоник.

- фазовая характеристика спектральной плотности (ФЧХ)- характеризует распределение по спектру фаз гармоник.

Теорема Парсеваля устанавливает распределение энергии по спектру:

, (4.4)

где - энергетическая спектральная плотность сигнала.

Весьма важными являются следующие свойства преобразований Фурье:

Преобразования Фурье линейны

если s(t)=s₁(t)+ s₂(t)++ s_p (t),

то S(iw)= S₁(iw)+ S₂(iw)++ S_p(iw).

Теорема запаздывания.

Если S(iw)  s(t), то для s(t-t₀) .

Спектр задержанного на t₀ сигнала отличается от исходного сдвигом фаз гармоник на величину =-wt₀.

Обратно: если всем составляющим спектра функции s(t) дать сдвиг на –wt₀, то функция преобразуется в s(t-t₀).

Теорема смещения.

Если S(iw)  s(t), то для функции, смещенной по спектру на величину w₀

, спектр равен , то есть все спектральные характеристики исходной функции смещаются на w₀.

Преобразования Фурье проводят анализ сообщений и сигналов в частотную область. Для исследования сигналов во временной области применяется разложение Котельникова В.А. (теория отсчетов).

Теорема Котельникова гласит:

Если функция s(t) не содержит частот выше Fm, то она полностью определяется последовательностью своих значений в моменты, отстающие друг от друга на . (см. Рис. 4.3.)

s(t)

t

∆t

(Рис. 4.3.)

В формализованном виде:

, (4.5.)

где wm=2Fm .

Для сообщений (сигналов) с ограниченной длительностью T и полосой Fm число учитываемых отсчетов

(4.6)

В большинстве случаев 1, поэтому

N=2FmT. (4.7)

Число N называют базой сигнала, или числом степеней свободы его. Оно определяет потенциальные возможности сигнала по переносу информации.

Энергия сигнала, выраженная через свои отсчеты по Котельникову, равна

, (4.8)

где 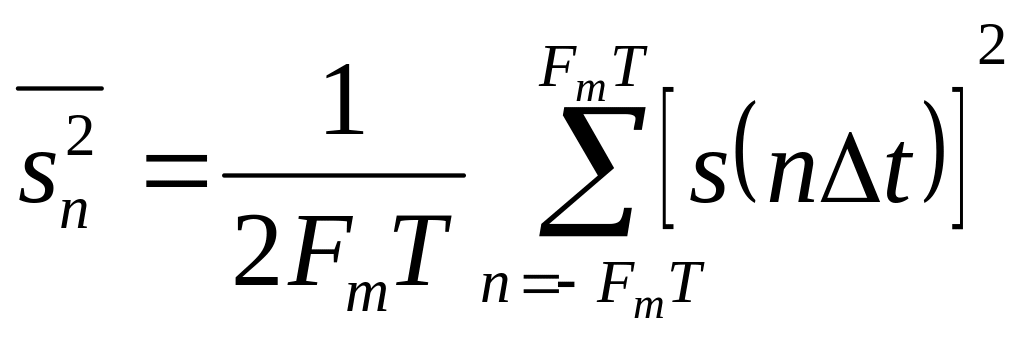- средняя мощность отсчета.

По теореме Котельникова можно представлять функции от любого параметра, не только от времени. В частности, можно представить рядом Котельникова спектральную плотность S(iw):

Если длительность сигнала не превышает Т, то спектральная плотность сигнала S(iw) полностью определяется последовательностью своих значений в точках на оси частот, отстающих одна от другой на расстоянии .

Относительно исходной теоремы здесь произошла замена параметров: t на w, ∆t на ∆w, wm на T/2.

Таким образом, математические модели сообщений и видеосигналов имеют одинаковую структуру и параметры и пригодны для анализа непрерывных и дискретных сообщений. Однако в них не учитывается корреляционные связи между сообщениями, существующие в языках общения людей. Корреляция (взаимосвязь) существует не только между соседними сообщениями. Она охватывает ν сообщений, что приводит к информационной избыточности.

Избыточность оценивается коэффициентом:

(4.9)

где энтропия системы сообщений при наличии взаимосвязи между ν сообщениями.

Исследования показали, что в русском языке при учете взаимосвязи только между соседними сообщениями (буквами алфавита) H1(x)=4.05 бит/сообщение. При ν=2 величина H2(x)=3,52 бит/сообщение. При ν=3 величина H3(x)=2,97 бит/сообщение. А при независимых сообщениях H0(x)=5 бит/сообщение. Поэтому R1(x)≈19%; R2(x)≈ 30%; R3(x)≈41%. Наличие естественной избыточности языка повышает помехоустойчивость сообщений при передаче их, но неэкономично расходует канальные ресурсы, объемы машинной памяти, время на анализ при обработке и т.д.

Исследование источников информации с корреляционными сообщениями удобно проводить с использованием аппарата цепей Маркова. Марковские источники характеризуются состоянием и правилами перехода из одного состояния в другое. Для них характерно, что вероятность любого состояния системы в будущем зависит только от состояния ее в настоящий момент и не зависит от того, каким образом система пришла в это состояние, то есть не зависит от предыстории.

Если передаются буквы, то состояние источника сообщений определяется передаваемой буквой: состояния SА , SБ ,…, SЯ. Например, говорят, что источник находится в состоянии передачи буквы Д, Ш или Ю. Вероятность появления последующей буквы зависит только от настоящего состояния. Вероятности переходов из состояния в состояние удобно анализировать на диаграммах (Рис. 4.4).

P(A/A) Р(Я/А)

P(Б/А) Р(Я/Б)

S_А S_Б S_Я

Рис. 4.4

Вероятность перехода, например Р(Я/А) – из состояния SА в состояние SЯ – отличается от Р(Я/Б).

Если вероятность появления букв не меняется от состояния, то можно говорить о том, что источник находится в одном стабильном состоянии S и корреляционных связей между сообщениями нет.

В этом случае диаграмма состояний имеет вид, показанный на рис. 4.5:

P(A) P(1)

P(Б)

S или S

Р(Я) P(0)

Рис. 4.5.

Если в системе с двумя состояниями (1 и 0) вероятности появления единиц и нулей различны, то диаграмма будет другой (рис. 4.6)

Р(0/0) Р(1/0) Р(1/1)

S₀ S₁

P(0/1)

Рис. 4.6.

Для анализа подобных источников надо знать вероятности состояний P(Sk) и вероятности переходов P(xi/Sk) для всех i и k.

Для бинарной системы, когда х1=0, х2=1, P(х1)=P(S1); P(х2)=P(S2), энтропия источника определяется следующим образом. Сначала фиксируется состояние S1 и определяется условная энтропия

,

потом аналогично определяется условная энтропия

.