20. В чем суть статистической значимости коэффициентов регрессии?

Как и в случае парной регрессии, статистическая значимость коэффициентов множественной линейной регрессии с m объясняющими переменными проверяется на основе t-статистики:

имеющей в данной ситуации распределение Стьюдента с числом степеней свободы ν = n-m-1 (n — объем выборки, m — количество объясняющих переменных в модели).(при парной регрессии число стtпеней свободы равно n-2) При требуемом уровне значимости наблюдаемое значение t-статистики сравнивается с критической точкой t_крит= t_α/2, n-m-1 распределения Стьюдента.

Если |t | > t_крит , то коэффициент bj считается статистически значимым. В противном случае (|t | <= t_крит ) коэффициент bj считается статистически незначимым (статистически близким к нулю). Это означает, что фактор Xj линейно не связан с зависимой переменной Y. Его наличие среди объясняющих переменных не оправдано со статистической точки зрения. Он не оказывает сколько-нибудь серьезного влияния на зависимую переменную, а лишь искажает реальную картину взаимосвязи. Если коэффициент bj статистически незначим, рекомендуется исключить из уравнения регрессии переменную Xj. Это не приведет к существенной потере качества модели, но сделает ее более конкретной.

21. Как определяется статистическая значимость коэффициентов регрессии

Проверка гипотезы ( ), (гипотеза о статистической значимости коэффициента регрессии).

Если Н₀ принимается, то есть основания считать, что исследуемая величина Y не зависит от Х. В этом случае коэффициент считается статистически незначимым (близким к нулю). При отклонении Н₀ (принятии Н₁) коэффициент признается статистически значимым, что указывает на наличие определенной линейной зависимости между Y и Х.

Оценка с помощью t-критерия Стьюдента значимости коэффициентов b1 и b2 связана с сопоставлением их значений с величиной их случайных ошибок: Sb1 и Sb2 аналогично

- стандартная ошибка регрессии

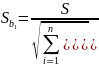– стандартная ошибка; 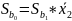- коэффициент регрессии

Чтобы сделать вывод о статистической значимости , рассчитывается соответствующее наблюдаемое значение t_набл по формуле и сравнивается с критическим значением t_кр при выбранном уровне значимости α и числе степеней свободы в парной регрессии n  2 (t_{α, n  2}) (Во множественной регрессии распределение Стьюдента с числом степеней свободы v = n  m  1 (n – объем выборки, m – число объясняющих переменных в модели). Если |t_набл| > t_кр, то гипотеза Н₀ отклоняется и коэффициент признается статистически значимым.

Коэффициент регрессии может изменяться в пределах

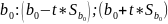
21. Что такое предсказание значения зависимой переменной? Как его найти?

В общем случае прогнозирование представляет собой задачу оценки зависимой переменной Y для некоторого набора объясняющих переменных, не входящих в область наблюдаемых статистических данных

С помощью интервальных оценок, построенных с заданной надежностью (1 –α), для конкретного значения х0можно построить доверительный интервал для условного математического ожидания (среднего значения) Y

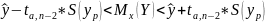
– для парной регрессии;

- средняя квадратическая ошибка рассчитанных по модели (прогнозируемых) значений 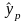, записанная в матричной форме для множественной регрессии.

Ошибка прогнозного значения и доверительный интервал для прогнозного значения

Прогнозное значение в точке х₀ обозначим через

Ошибка прогноза

– для парной регрессии;

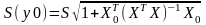- для множественной регрессии.

Доверительный интервал для прогноза

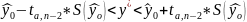
Доверительный интервал для прогнозного значения – это интервал, который с надежностью(вероятностью) 1-α показывает истинное значение объсняемой переменной y, которую принимает при x=