
- •Эконометрика. Цели и задачи. Этапы эконометрического моделирования.
- •Основные этапы регрессионного анализа.
- •Что такое функция регрессии? Чем регрессионная модель отличается от функции регрессии?
- •Как выглядит линейная модель парной регрессии? Как называются переменные в модели?
- •Коэффициент корреляции. Свойства коэффициента корреляции. Множественный коэффициент корреляции. Частный коэффициент корреляции. Ложная корреляция.
- •Причины наличия в регрессионной модели случайного отклонения.
- •Что понимается под спецификацией модели и как она осуществляется в случае одной независимой переменной.
- •В чем состоит различие между теоретическим и эмпирическим уравнениями регрессии?
- •В чем суть метода наименьших квадратов?
- •Выведите формулы для расчета коэффициентов парной линейной регрессии по методу наименьших квадратов.
- •Проинтерпретируйте коэффициенты эмпирического парного линейного уравнения регрессии.
- •12.Коэффициент детерминации. Роль коэффициента детерминации при определении качества построенного уравнения регрессии. Формула расчёта коэффициента детерминации.
- •15. Расчет коэффициентов множественной регрессии по мнк в матричной форме.
- •16. Коэффициент детерминации и скорректированный коэффициент детерминации.
- •Сформулируйте предпосылки мнк. Каковы последствия их выполнимости или невыполнимости.
- •Как определяются стандартные ошибки регрессии и коэффициентов регрессии?
- •19. Интервальные оценки коэффициентов регрессии
- •20. В чем суть статистической значимости коэффициентов регрессии?
- •Как определяется статистическая значимость коэффициентов регрессии
- •Что такое предсказание значения зависимой переменной? Как его найти?
- •Что означает статистическая значимость уравнения регрессии в целом? Как проверить значимость уравнения по f-тесту?
- •Что такое мультиколлинеарность? Последствия мультиколлинеарности.
- •Методы устранения мультиколлинеарности.
- •26. Пошаговый метод включения исключения факторной переменной в модель регрессии.
- •27.Нелинейные модели регрессии.
- •28.Основные виды ошибок спецификации модели.
- •4.3. Ошибки спецификации
- •29. Фиктивная переменная. Причины использования фиктивных переменных в моделях регрессии.
- •Что такое автокорреляция остатков, и каковы ее виды? Причины ее возникновения.
- •30. В чем суть теста Чоу проверки структурной однородности модели. Тест Грегори Чоу
- •Примеры использования фиктивных переменных.
- •Каким образом выявляется наличие автокорреляции в остатках?
- •Способы устранения автокорреляции в остатках.
- •Что такое гетероскедастичность? Причины и последствия гетероскедастичности.(гл 5)
- •38. Временной ряд. Составляющие временного ряда. Примеры.
- •39.Коэффициент автокорреляции. Автокорреляционная функция. Коррелограмма.
Причины наличия в регрессионной модели случайного отклонения.
Y
= M
(Y|X)
+

– случайное отклонение
Причины:
Не включение в модель всех объясняющих переменных.
Не правильный выбор функциональной формы модели.
Ошибки измерений.
Ограничение стат. Данных.
Человеческий фактор
Что понимается под спецификацией модели и как она осуществляется в случае одной независимой переменной.
Спецификация модели — один из этапов построения экономико-математической модели, на котором на основании предварительного анализа рассматриваемого экономического объекта или процесса в математической форме выражаются обнаруженные связи и соотношения, а значит, параметры и переменные, которые на данном этапе представляются существенными для цели исследования. Иными словами, С. м. есть выбор формулы связи переменных. Напр., в случае регрессионного анализа выбирается формула регрессии, подходящая для обнаруженных сочетаний независимых и зависимых переменных — линейная, квадратичная или иная.
От правильно выбранной спецификации модели зависит величина случайных ошибок – они тем меньше, чем в большей мере теоретические значения результативного признака подходят к фактическим данным.
В чем состоит различие между теоретическим и эмпирическим уравнениями регрессии?
Теоретическое уравнение регрессии (гипотетически для генеральной совокупности):
Y=
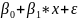
где
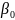 – свободный коэффициент;
– свободный коэффициент;
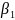 -
коэффициент регрессии;
-
коэффициент регрессии;
ε – случайное отклонение (возмущение).
Случайное отклонение включает влияние не учтенных в модели факторов, случайных ошибок и особенностей измерения. Источники его присутствия в модели: спецификация модели, выборочный характер исходных данных, особенности измерения переменных.
Эмпирическое уравнение регрессии (для выборки наблюдений):
 =
=

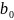 –
эмпирическая
(выборочная) оценка свободного
коэффициента;
–
эмпирическая
(выборочная) оценка свободного
коэффициента;
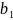 -
эмпирическая (выборочная) оценка
коэффициента регрессии;
-
эмпирическая (выборочная) оценка
коэффициента регрессии;
В чем суть метода наименьших квадратов?
Суть метода наименьших квадратов (МНК) - оценки параметров таковы, что сумма квадратов отклонений фактических значений зависимой переменной Yi от расчетных (теоретических) Yx минимальна.
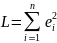
Выведите формулы для расчета коэффициентов парной линейной регрессии по методу наименьших квадратов.

Проинтерпретируйте коэффициенты эмпирического парного линейного уравнения регрессии.
По реальным наблюдениям (по выборке ограниченного объема) мы сможем построить так называемое эмпирическое уравнение регрессии.
![]() ,
,
где
Ŷ
оценка
условного математического ожидания
Мх(Y),
![]() и
и
![]()
оценки неизвестных теоретических
параметров модели b0
и b1,
называемые эмпирическими коэффициентами
регрессии. Следовательно, для конкретных
значений yi
в случае эмпирической парной модели
справедливо следующее соотношение:
оценки неизвестных теоретических
параметров модели b0
и b1,
называемые эмпирическими коэффициентами
регрессии. Следовательно, для конкретных
значений yi
в случае эмпирической парной модели
справедливо следующее соотношение:
![]() ,
,
где отклонение (остаток) ei представляет собой оценку теоретического случайного отклонения еi.
Линейная регрессионная модель является наиболее распространенным и удобным для анализа видом зависимости между экономическими переменными. Простейшее парное уравнение позволяет достаточно наглядно (часто с помощью графической интерпретации) рассмотреть основные приемы регрессионного анализа. Кроме того, парная регрессия может служить начальной точкой эконометрического моделирования.
13.Как оценивается качество уравнения регрессии с помощью относительной ошибки аппроксимации?
Наряду
с коэффициентом детерминации R2
для оценки качества парной регрессионной
модели можно использовать характеристику,
называемую средней
ошибкой аппроксимации
![]() :
:
 %.
%.
Средняя ошибка аппроксимации определяет среднее относительное отклонение расчетных данных (оцененных по уравнению модели) от фактических. является безразмерной величиной и обычно выражается в процентах. Принято считать, что качество модели считается удовлетворительным, если средняя ошибка аппроксимации не превышает 89 %.
