18. Оценка параметров уравнения множественной регрессии.
Параметры уравнения множественной регрессии оцениваются МНК.
Для отыскания параметров сроится система нормальных уравнений.
y = a +
+
+
+ … +
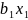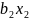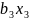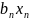
Тогда система нормальных уравнений принимает следующий вид:
∑y = na +
+
+
+
… +
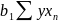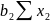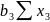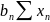
∑y ∙
=
+
+
∙
+
∙
+ … +
∙
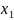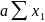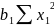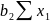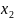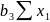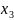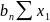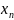
∑y ∙
=
+
∙
+
+
∙
+ … +
∙
…
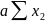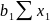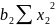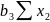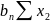∑y ∙
=
+
∙
+
∙
+
∙
+ … +
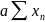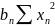
Эту систему можно записать в следующем виде:
А
= (a;
;
;
)
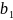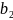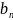Y=
Х = А ∙ У А = У ∙
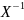
Если функция степенная, или другая нелинейная, то её сначала линеализуют, а затем применяют МНК.
19. Стандартизованный коэффициент регрессии
Стандартизованный
коэффициент регрессии 
,
используют для сравнения влияния на
зависимую переменную различных
объясняющих переменных. Он показывает,
на сколько величин sy изменится
в среднем зависимая переменная y при
увеличении только i-ой
переменной на 
.
Построение модели множественной регрессии в стандартизированном или нормированном масштабе означает, что все переменные, включенные в модель регрессии, стандартизируются с помощью специальных формул.
Посредством процесса стандартизации точкой отсчёта для каждой нормированной переменной устанавливается её среднее значение по выборочной совокупности. При этом в качестве единицы измерения стандартизированной переменной принимается её среднеквадратическое отклонение .
Факторная переменная х переводится в стандартизированный масштаб по формуле:
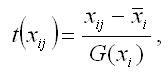
где xij – значение переменной xjв i-том наблюдении;
G(xj) – среднеквадратическое отклонение факторной переменной xi;
Результативная переменная у переводится в стандартизированный масштаб по формуле:
где G(y) – среднеквадратическое отклонение результативной переменной у.
Если между исследуемыми переменными в исходном масштабе является линейной, то процесс стандартизации не нарушает этой связи, поэтому стандартизированные переменные будут связаны между собой линейно:
Неизвестные коэффициенты данной функции можно определить с помощью классического метода наименьших квадратов для линейной модели множественной регрессии. В этом случае минимизируется функционал F вида:
В результате минимизации данного функционала получим систему нормальных уравнений, переменными в которой будут являться парные коэффициенты корреляции между факторными и результативной переменной. Такой подход основывается на следующем равенстве:
Система нормальных уравнений для стандартизированной модели множественной регрессии имеет вид:
20. Множественная корреляция
Практическая значимость уравнения множественной регрессии оценивается с помощью показателя множественной корреляции и его квадрата – коэффициента детерминации. Показатель множественной корреляции характеризует тесноту связи рассматриваемого набора факторов с исследуемым признаком, или, иначе, оценивает тесноту совместного влияния факторов на результат.
Независимо от формы связи показатель множественной корреляции может быть найден как индекс множественной корреляции:
=
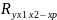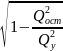
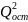-общая
дисперсия результативного признака;
-
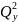остаточная дисперсия для уравнения у
= f(x1,x2,
… ,xp).
Методика построения индекса множественной корреляции аналогична построению индекса корреляции для парной зависимости. Границы его изменения те же: от 0 до 1, чем ближе его значение к 1, тем теснее связь результативного признака со всем набором исследуемых факторов. Величина индекса множественной корреляции должна быть больше или равна максимальному парному индексу корреляции:
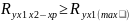(1=1,p)
При правильном включении факторов в регрессионный анализ величина индекса множественной корреляции будет существенно отличаться от индекса корреляции парной зависимости. Если же дополнительно включенные в уравнение множественной регрессии факторы третьестепенны, то индекс множественной корреляции может практически совпадать с индексом парной корреляции. Отсюда ясно, что, сравнивая индексы множественной и парной корреляции, можно сделать вывод о целесообразности включения в уравнение регрессии того или иного фактора.
Можно воспользоваться следующей формулой индекса множественной корреляции:
