2.4 Марковские ветвящиеся процессы (вероятность заражения компьютера пользователя социальной информационной сети)

Рассмотрим случайную функцию Z(t), описывающую количество зараженных компонентов автоматизированной системы (ЗКАС). Эта функция принимает неотрицательные целые значения. Если количество ЗКАС известно в некоторый момент времени Z(t₁) = k, то предполагается, что дальнейший процесс заражения компонент (ЗК) определяется законом распределения вероятностей, зависящим от tи, возможно, от абсолютного времени, но не зависит от свойств процесса заражения до времени t₁ , т.е. ЗК является марковским процессом [120].

Будем рассматривать Z(t) исключительно в терминах переходных вероятностей . При изучении переходных вероятностей будут использованы прямое и обратное дифференциальные уравнения Колмогорова, которым удовлетворяют эти вероятности. Данные вероятности могут быть записаны, как только будут заданы соответствующие функции b_i(t) и p_ij(t), i, j = 0, 1, 2, …. Если Z(t) = i, то вероятность изменения состояния в интервале равна , где - бесконечно малая функция, которая стремится к нулю, при . Если известно, что изменение произошло в момент t, причем до изменения состоянием процесса было i (компонента автоматизированной системы (КАС) не заражена), то p_ij(t) равно вероятности того, что новым состоянием будет j (КАС заражена) [83, 84].

Предположим, что некоторая КАС, существующая в момент времени t, заражается в интервале с вероятностью , где b – некоторая непрерывная строго положительная функция. Если она заражается в момент , то с вероятностями возникает 0, 1, 2, 3, ... новых ЗКАС.

Отметим, что если КАС заражается в момент t₁ , то плотность распределения вероятностей времени заражения имеет вид

;

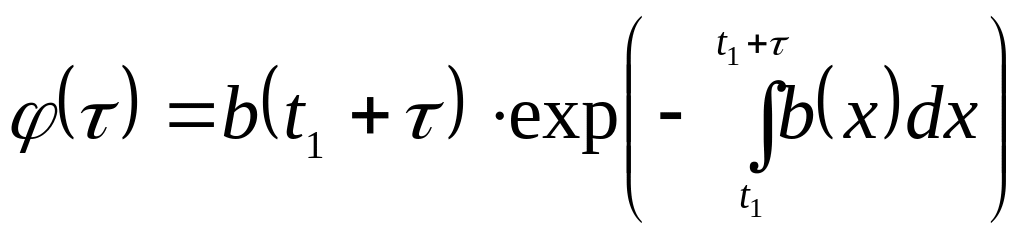при постоянном b это показательная функция.

Если в момент t существует i независимых КАС, то вероятности того, что в интервале не заразится ни одной КАС, заразится одна КАС или не меньше двух, равны (соответственно по формуле биномиального распределения): и . Если количество ЗКАС состояло из i КАС и в момент заразилась одна КАС, то вероятность того, что новое количество ЗАС состоит из j АС равна, . Таким образом показано, что можно определить величины и . Тогда прямая и обратная системы уравнений Колмогорова имеют вид (2.4.3) и (2.4.4).

Марковским ветвящимся процессом называется цепь Маркова, состояниями которой являются целые неотрицательные числа и переходные вероятности которой задаются решением прямой системы уравнений (2.4.3). Тогда, как мы увидим, эти вероятности автоматически будут решением обратной системы уравнений (2.4.4). Предполагается, что b – непрерывная строго положительная функция, p_i непрерывны и неотрицательны, и . Если b и p_i не зависят от t, то говорят, что процесс однороден во времени [83, 84].

Замечание 1. Допускаем возможность того, что при . Этот случай соответствует тому, что Z может принимать значение на конечном отрезке времени. В таких случаях обратная система уравнений имеет решения, не удовлетворяющие прямо системе; эти решения уже не обладают свойством независимости, характерным для истинных ветвящихся процессов. Прямой системе удовлетворяет только одно множество переходных вероятностей.

Замечание 2. Для некоторого упрощения изложения будем считать, что .

Пусть Z(t) является марковским ветвящимся процессом с переходными вероятностями

; . (2.4.1)

Вследствие марковской природы этого процесса переходные вероятности (3.4.1) удовлетворяют уравнениям Колмогорова – Чепмена:

; . (2.4.2)

При изучении вероятностей P_ik будем использовать прямую и обратную системы дифференциальных уравнений для марковских процессов в том специальном виде (см. Замечание 1). Прямой системой уравнений является система

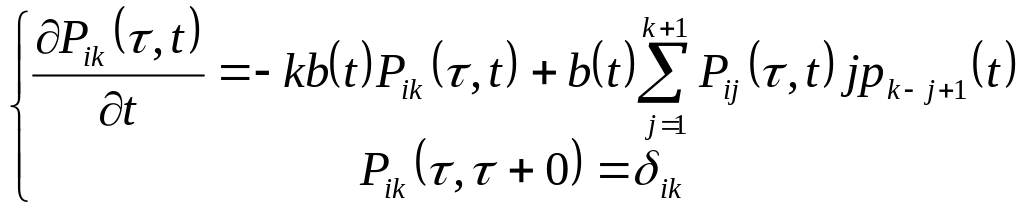; (2.4.3)

(здесь при и при ). Обратная система имеет вид

Множество функций , является решением системы (2.4.3) или (2.4.4), если эти функции неотрицательны, абсолютно непрерывны и по и по t. Эти функции удовлетворяют уравнениям (2.4.2) и неравенству:

. (2.4.5)

Из результатов Феллера [92] следует, что всегда имеется решение , общее для систем (2.4.3) и (2.4.4). Любое решение системы (2.4.3) обладает свойством

. (2.4.6)

Смысл равенства (2.4.6) заключается в том, что число i ЗКАС, существовавших в момент , к моменту времени t распределена как сумма i независимых множеств ЗКАС, каждое из которых возникла из одной ЗКАС [120].

Вопрос единственности решения системы (2.4.4) представляет особый интерес, так как он связан со справедливостью формулы (2.4.6), а также с вопросом о наличии знака равенства в соотношении (2.4.5).

Феллер изучал цепи [92]для которых в (2.4.5) имеет место строгое неравенство при . В нашем случае строгое неравенство может наступить, если Z(t) будет возрастать так быстро, что станет бесконечным за конечное время. Назовем этот случай взрывом [98].

Если в (2.4.5) имеет место строгое неравенство, то, как было показано Дубом[93], существует целое семейство процессов, удовлетворяющих обратным уравнениям Колмогорова ((2.4.4) в нашем случае). Мы получим такой процесс, если всякий раз, когда Z(t) принимает значение , будем считать, что процесс начинается снова с некоторого конечного значения. Существует много способов выбрать начальное значение для продолжения процесса. Следовательно, если существует решение, для которого , то система (2.4.4) имеет бесконечно много решений, хотя система (2.4.3) имеет по-прежнему только одно решение. В случае, когда решение системы (2.4.3) удовлетворяет тождеству , система (2.4.4) имеет единственное решение. Однако всегда имеется только одно решение системы (2.4.4), удовлетворяющее соотношению (2.4.6), т. е. решение, которое обладает характеристическим свойством ветвящихся процессов [120].

Пусть мы имеем случай взрыва с Z(0) = 2, и пусть продолжение процесса осуществляется следующим способом (одним из многих возможных). Всякий раз, когда Z(t) принимает значение , процесс немедленно возвращается в состояние 2 и начинается снова.

Вероятности для такого продолженного процесса удовлетворяют обратным уравнениям и не удовлетворяют прямым [83, 84].

Для продолженного процесса соотношение (2.4.6) теперь не выполняется, т. е. различные ветви всей совокупности не ведут себя как независимые. Действительно, сначала процесс, начавшийся с Z(0) = 2 развивается так же, как два независимых процесса, начавшихся с Z(0) = 1. Однако, как только какая-либо из двух ветвей уйдет в бесконечность, по нашему правилу требуется, чтобы всё сообщество вернулось в состояние 2. Следовательно, взрыв в одной ветви влияет на другую ветвь, и различные частицы уже не независимы.

Если является решением системы (2.4.3), то

.

Предположим, что является любым решением системы (2.4.3). Пусть , , где p_i —функции, введенные в определении марковских процессов.

Пусть

, (2.4.7)

где функции P_ik— некоторое решение системы (2.4.3).

Замечание: допустим возможность того, что при это соответствует случаю взрыва.

Если мы умножим обе части системы (2.4.3) на s^k и просуммируем по k, то формально мы получим уравнения

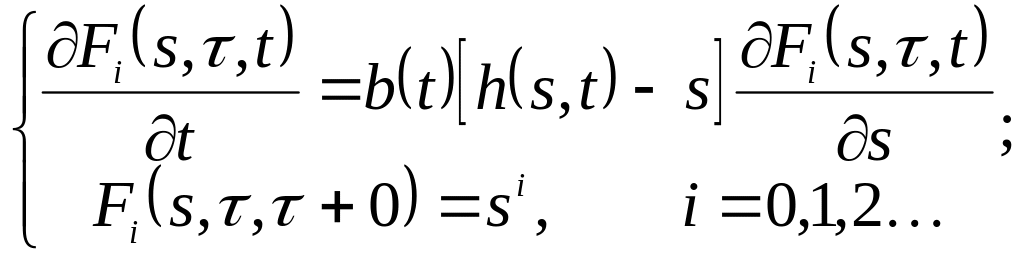(2.4.8)

Справедлива следующая теорема: существует только одно решение системы (2.4.3). Производящие функции F_i , определенные формулой (2.4.7), удовлетворяют уравнениям (2.4.8) при кроме того, . Таким образом, свойство ветвящихся процессов (2.4.6) выполняется.

Из результатов Феллера[92] известно, что решение системы (2.4.3), о котором теперь известно, что оно единственно, должно также удовлетворять системе (2.4.4). Положим i = 1 в (2.4.4), умножим обе части на s^k и просуммируем по k. Используя соотношение формально получаем

, (2.4.9)

Имеет место следующий результат, относящийся к системе уравнений (2.4.4).

Система (2.4.4) имеет только одно решение, которое обладает свойством ветвящихся процессов (2.4.6), и это решение является единственным решением системы (2.4.3). Производящая функция F₁, определенная формулой (2.4.7) при i = 1, удовлетворяет уравнению (2.4.9) при .

В дальнейшем будет полезно следующее свойство функции F₁. Предположим, что . Производящая функция F₁, удовлетворяет неравенству . Если и t находятся в конечном интервале, то существует такая постоянная с, 0<c<1, что выполняется неравенство .

Следующее простое условие приводит к тому, что единственное решение системы (2.4.3) удовлетворяет тождеству . В этом случае, это решение является также единственным решением системы (2.4.4).

Условие: ряд сходится равномерно по t в каждом конечном интервале.

Докажем, что сумма вероятностей равна 1. Пусть t фиксировано, и пусть . Тогда удовлетворяет обыкновенному дифференциальному уравнению , где G(t-0)=1 и . В силу определения функции h правая часть этого дифференциального уравнения удовлетворяет условию Липшица в области , . Следовательно, решение единственно, а так как 1 является решением, то .

Согласно результатам Феллера [92], решение системы (2.4.3) является минимальным решением системы (2.4.4) в том смысле, что любое другое решение удовлетворяет неравенствам . Так как

,

то .

Условие является наиболее простым условием, предупреждающим такой быстрый рост ЗАС, при котором за конечное время группа пользователей становится бесконечной.

Производящая функция F₁ обладает следующим свойством.

Пусть производящая функция определяется формулой (2.4.7) при i=1. Тогда она удовлетворяет функциональному соотношению:

. (2.4.10)

Пусть теперь условие выполнено, так что является производящей функцией вероятностей в обычном смысле. Для простоты рассмотрим случай однородных во времени процессов, для которых . Пусть - фиксированное положительное число, ; Z(t) - марковский ветвящийся процесс, соответствующий F₁, и пусть Z(0) — произвольное неслучайное целое число. Используя однородность процесса во времени и соотношение , получаем

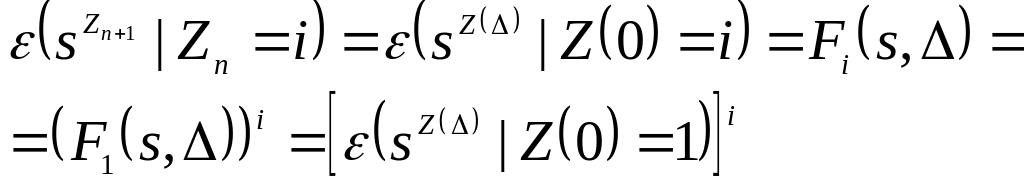. (2.4.11)

Соотношение (2.4.11) выражает свойство, определяющее процесс Гальтона — Ватсона; следовательно, последовательность является процессом Гальтона — Ватсона. Таким образом, производящая функция является n-й итерацией функции ; этот факт можно также получить из соотношения (2.4.10) [120].

Если процесс не однороден во времени или если мы рассматриваем последовательность , где t_i не равноудалены, то имеют место аналогичные результаты, только мы должны рассматривать процесс Гальтона — Ватсона с переменной производящей функцией [83,84].

Рассмотрим случай однородного во времени процесса, для которого b(t) = b = const, h(s,t) = h(s) и . В этом случае вместо (2.4.10) имеем

. (2.4.12)

Отметим, что является n-й итерацией функции ; обозначим последнюю функцию через f(s). Так как соотношение (2.4.12) выражает характеристическое свойство итераций, когда t₁ и t₂— целые числа, то мы можем рассматривать при нецелом t как дробную итерацию функции f.

Классическая задача анализа заключается в следующем. Дана функция f(s), требуется найти функцию , удовлетворяющую условию и соотношению (2.4.12). Кёнигс показал, как может быть решена эта задача, если f аналитична в окрестности фиксированной точки s₀, f(s₀) = s₀ и . Можно показать, что предел

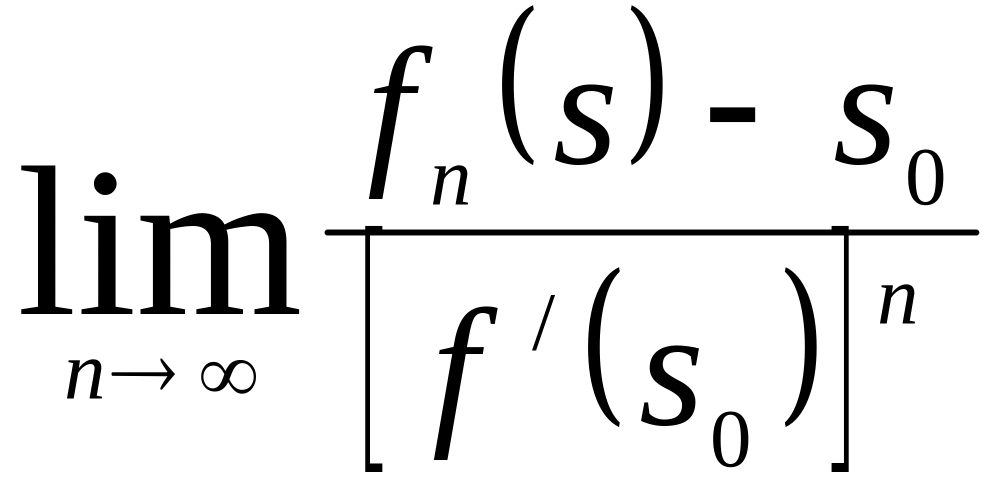
существует при s, близких к s_o обозначим его A(s). Тогда А удовлетворяет функциональному уравнению , откуда и . Последнее выражение может служить определением итераций f_n при нецелом n. Другой подход основан на использовании функционального уравнения Абеля.

Если f является производящей функцией вероятностей, то естественно выяснить, можно ли найти такую функцию F(s,t); удовлетворяющую соотношению (2.4.12), что она будет производящей функцией вероятностей при каждом t. Мы также наложим еще некоторое условие регулярности; потребуем, чтобы предел

(2.4.13)

существовал равномерно по . Если можно найти такую функцию F, то мы будем говорить, что f принадлежит классу С.

Если f принадлежит классу С и если , то можно показать, что функция должна быть степенным рядом вида , b > 0, , используя (2.4.12) и (2.4.13) и полагая или , получаем соответственно

(2.4.14)

и

. (2.4.15)

Эти уравнения являются уравнениями для производящей функции марковского ветвящегося процесса, однородного во времени. Таким образом, если f принадлежит классу С, то процесс Гальтона — Ватсона, соответствующий f, может быть вложен в марковский ветвящийся процесс.

Если мы предположим F(s,1) = f(s) и приравняем правые части равенств (2.4.14) и (2.4.15), то получим функциональное уравнение

. (2.4.16)

Если f принадлежит классу С (в этом случае можно пока­зать, что ) и если f(0)=0, то из (2.4.16) следует, что p₀ = 0 и коэффициенты p₂, p₃,… можно определить повторным дифференцированием уравнения (2.4.16) в точке s = 0.

Очевидно, что многие производящие функции f не принадлежат классу С, например многочлены степени 2 и выше [98].

Если f — производящая функция с f(0)=0 и , то можно показать, что необходимым и достаточным условием принадлежности f классу С является неотрицательность чисел , определяемых дифференцированием уравнения (2.4.16). Кроме того, если f — целая функция и f(0)=0, то можно показать, что f не принадлежит классу С. Однако общая задача определения принадлежности f классу С еще не решена [120].

Определим k-й факториальный момент формулой

Если ряд сходится равномерно по t в каждом конечном интервале, то момент m_k(,t) конечен и может быть определен из уравнения, полученного дифференцированием (2.4.8) или (2.4.9) k раз по s в точке s = 1. Например, для m₁ имеем

. (2.4.17)

Если k>1, то m_k(t-0,t) = 0.

Решением уравнения (2.4.17) является

. (2.4.18)

Приведем формулы первых двух моментов для однородных во времени процессов.

Предположим для однородных во времени процессов .

Теорема: в случае однородных во времени процессов с Z(0) = 1 имеем

, (2.4.19)

, (2.4.20)

. (2.4.21)

Рассмотрим марковский ветвящийся процесс на примере заражения компьютеров пользователей СИС, определяемый следующим образом. Предположим, что любая АС, существующая в момент времени t, с вероятностью заражается в интервале и с вероятностью в том же интервале подвергает заражению две новые АС. Для процесса заражения имеем при i=1 или i>2, , и [83,84].

Мы всегда предполагаем, что функция b строго положительна, хотя можно рассмотреть и противоположный случай. Уравнение (2.4.9) становится теперь уравнением Риккати:

;

. (2.4.22)

Решение уравнения (2.4.22) было получено Кендаллом[91]. Положив

,

,

.

Кендалл показал, что решение уравнения (2.4.22) можно записать в виде

. (2.4.23)

Отсюда для вероятностей получаем следующие выражения:

, n=1, 2, . . . (2.4.24)

Если , то первый момент равен ,а дисперсия равна .

Из формул (2.4.24) и определения следует, что вероятность вырождения равна 1 (т. е. при каждом ) тогда и только тогда, когда .