- •Вопрос 1.Гипотезы, применяемые в сопромате.
- •Вопрос 2.Определение внутренних силовых факторов. Метод Сечений.
- •Вопрос 3.Напряжения при растяжении (сжатии). Условия прочности.
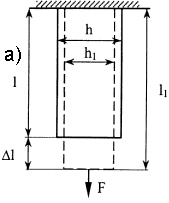
- •Вопрос 4.Деформация при растяжении(сжатии). Определение перемещений.
- •Вопрос 5. Статически неопределимые системы, работающие на растяжение (сжатие).
- •Вопрос 6.Механические свойства материалов. Пластическое и хрупкое разрушение.
- •Вопрос 7.Допускаемые напряжения для пластичных и хрупких материалов.
- •8.Геометрические характеристики плоских сечений. Определение координат центра тяжести фигуры.
- •Вопрос 9.Зависимость моментов инерции при параллельном переносе осей и их повороте относительно начала координат.
- •Вопрос 10.Геометрические характеристики простейших фигур
- •Вопрос 11.Кручение. Гипотезы. Касательные напряжения при кручении. Эпюра касательных напряжений.
- •Вопрос 12.Условия жёсткости и прочности при кручении. Полярный момент сопротивления. Жёсткость поперечного сечения при кручении.
- •Вопрос 13.Определение углов поворота при кручении.
- •Вопрос 14.Статически неопределимые системы, работающие на кручение.
- •Вопрос 15.Изгиб, Виды изгиба, Внутренние силовые факторы, Эпюры поперечных сил и изгибающих моментов.
- •Вопрос 16.Формула кривизны нейтрального слоя.
- •Вопрос 17.Нормальные напряжения при изгибе. Условия прочности. Осевой момент сопротивления.
- •Вопрос 18.Определение перемещений при изгибе. Интеграл Мора. Метод Верещагина.
- •Вопрос 19.Косой изгиб. Условия прочности.
- •20.Рациональные типы поперечных сечений изгибающих элементов.
- •21.Внецентренное действие сил. Условие прочности.
- •22.Расчёт на устойчивость. Формула Эйлера
Вопрос 1.Гипотезы, применяемые в сопромате.
-Гипотеза сплошности и однородности: материал представляет собой однородную сплошную среду; свойства материала во всех точках тела одинаковы и не зависят от размеров тела.
-Гипотеза об изотропности материала: физ.- мех. свойства материала одинаковы по всем направлениям.
-Гипотеза об идеальной упругости материала: тело способно восстанавливать свою первоначальную форму и размеры после устранения причин, вызвавших его деформацию.
-Гипотеза о малости деформаций: деформации в точках тела считаются настолько малыми, что не оказывают существенного влияния на взаимное расположение нагрузок, приложенных к телу.
-Допущение о справедливости закона Гука: перемещения точек конструкции в упругой стадии работы материала прямо пропорциональны силам, вызывающим эти перемещения.
-Принцип независимости действия сил: результат воздействия нескольких внешних факторов равен сумме результатов воздействия каждого из них, прикладываемого в отдельности, и не зависит от последовательности их приложения.
-Гипотеза Бернулли о плоских сечениях: поперечные сечения, плоские и нормальные к оси стержня до приложения к нему нагрузки, остаются плоскими и нормальными к его оси после деформации.
Вопрос 2.Определение внутренних силовых факторов. Метод Сечений.
Внутренние силы – силы взаимодействия между частицами тела при деформации.
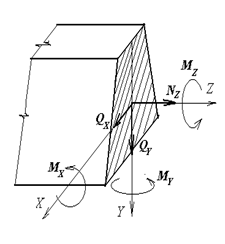
На примере бруса покажем ВСФ: Проекции главного вектора R и главного момента M на ГЛАВНЫЕ ЦЕНТРАЛЬНЫЕ ОСИ поперечного сечения и ПРОДОЛЬНУЮ ось бруса называются ВНУТРЕННИМИ СИЛОВЫМИ ФАКТОРАМИ (ВСФ) в поперечном сечении. ВСФ (см рис 1) обозначаются:
Nz = N - продольная растягивающая (сжимающая) сила
Mz = T - крутящий (скручивающий) момент
Qx (Qy) = Q - поперечные силы
Mx (My) = M - изгибающие моменты, Справа показаны уравнения, определяющие каждый всф:
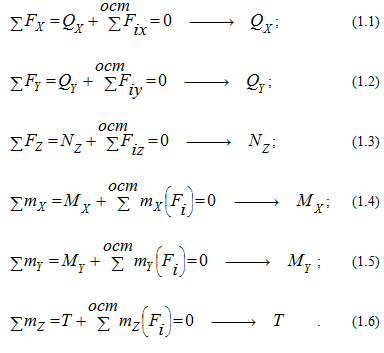
Метод сечений заключается в том, что тело мысленно рассекается плоскостью на две части, любая из которых отбрасывается и взамен ее к сечению оставшейся части прикладываются внутренние силы, действовавшие на нее до разреза со стороны отброшенной части. Оставленная часть рассматривается как самостоятельное тело, находящееся в равновесии под действием приложенных к сечению внешних и внутренних сил (третий закон Ньютона – действие равно противодействию). При применении этого метода выгоднее отбрасывать ту часть элемента конструкции (тела), для которой проще составить уравнение равновесия. Таким образом, появляется возможность определить внутренние силовые факторы в сечении, благодаря которым оставшаяся часть тела находится в равновесии (прием, часто применяемый в Статике). Если коротко, то имеет вид:
1.Рассечь тело плоскостью.
2.Отбросить одну из его частей.
3.Заменить на внутренний силовой фактор отброшенной частью.
4.Уравновесить.
Вопрос 3.Напряжения при растяжении (сжатии). Условия прочности.
Осевым растяжением (сжатием) брусьев называют такой вид деформирования, при котором в их поперечных сечениях возникает единственный внутренний силовой фактор – продольная сила Nz.
Для определения продольной силы используется метод сечений. Nz= Σ Fzвн
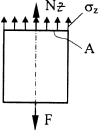
![]() Nz равномерно
распределяется по площади поперечного
сечения, вызывая нормальные напряжения(σz
– это напряжение).
Nz равномерно
распределяется по площади поперечного
сечения, вызывая нормальные напряжения(σz
– это напряжение).
Правило знаков для продольной силы: растягивающая продольная сила положительна, сжимающая – отрицательна.
Условие прочности при растяжении (сжатии) выражается неравенством: σmax =(Nmax / A) ≤ [σ],где [σ] – допускаемые напряжения, определяются как [σ] = σпред / n
![]()
n– коэффициент запаса прочности, устанавливаемый нормативными документами.
Условие прочности позволяет решать три типа задач:
1.Проверка прочности (проверочный расчет) σmax = (Nmax / A) ≤ [σ]
2. Подбор сечения (проектировочный расчет) A ≥ Nmax / [σ]
3.Определение грузоподъемности (допускаемой нагрузки) Nmax ≤ [σ] * A