2.1.2 Необходимые сведения

При классическом определении вероятность события определяется равенством

где m-число элементарных исходов испытания, благоприятствующих появлению события А; n - общее число возможных элементарных исходов испытания. Предполагается, что элементарные исходы образуют полную группу и равновозможны.

Относительная частота события А определяется равенством

где m-число испытаний, в которых событие А наступило;

n - общее число произведенных испытаний. При статистическом определении в качестве вероятности события принимают его относительную частоту при неограниченном увеличении числа испытаний. Решение задач по теории вероятностей на классическую схему часто облегчается за счет использования формул комбинаторики.

Если из множества, содержащего n элементов, каким-то способом отобраны m элементов (m ≤ n), то говорят, что из этого множества произведена выборка объема m.

Если порядок расположения элементов выборки принимают во внимание, то выборки называют упорядоченными. Таким образом, две упорядоченные выборки считаются различными, если они отличаются либо составом элементов, либо их расположением. В том случае, когда порядок расположения элементов не учитывают, выборки называют неупорядоченными. Следовательно, две неупорядоченные выборки считают различными, если в одной из них есть хотя бы один элемент, которого нет в другой.

Элементы в выборке могут повторяться, тогда она называется выборкой с повторениями. Если повторения запретить, получим выборку без повторений.

Размещения.

Всякая упорядоченная выборка объема m из множества,

содержащего n элементов (m ≤ n), называется размещением из n

элементов по m элементов без повторений.

Число размещений из n элементов по m задается равенством

Для удобства принято считать, что Условились, что 0!=1 и 1!=1.

Число размещений с повторениями из n предметов по m обозначается .

Справедлива формула .

Перестановки.

Размещением из n элементов по n элементов называются перестановками из n элементов.

Перестановки являются частным случаем размещений. Различные перестановки отличаются друг от друга только порядком элементов. Число перестановок из n элементов обозначают

через .

Сочетания.

Всякая неупорядоченная выборка объёма m из множества, содержащего n элементов (m ≤ n), называется сочетанием из n элементов по m элементов без повторений.

Число сочетаний из n элементов по m задаётся равенством

Некоторые свойства сочетаний.

Число сочетаний из n элементов по m с повторениями будем находить по формуле

При решении задач на подсчет числа выборок нужно ставить два вопроса:

1. возможны ли повторения выбираемых элементов?

2. важен ли порядок элементов?

В зависимости от ответов используют соответствующую формулу таблицы:

Выборка	Упорядоченная	Неупорядоченная
Без повторений
С повторениями

Теоремы сложения и умножения вероятностей.

События называются несовместными, если они не могут появиться вместе в одном опыте.

Если одно из событий произойдет обязательно, то такие события образуют полную группу.

Суммой событий называется событие, состоящее в появлении хотя бы одного из рассматриваемых событий.

Теорема сложения вероятностей несовместных событий:

Вероятность суммы попарно несовместных событий равна сумме вероятностей этих событий;

Сумма вероятностей событий, образующих полную группу, равна единице. Произведением событий называется событие, состоящее в появлении всех из рассматриваемых событий.

Вероятность события B, вычисленная при условии, что произошло событие А, называется условной вероятностью события В относительно события А. Эта вероятность обозначается или .

Теорема умножения вероятностей двух событий.

Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность второго относительно первого:

.

Эта теорема обобщается на любое конечное число событий:

Вероятность произведения нескольких событий равна произведению вероятности одного из них на условные вероятности всех остальных, причем вероятность каждого последующего события вычисляют в предположении, что все предыдущие события уже наступили;

.

Если появление одного из событий не влияет на вероятность появления другого, то такие события называются независимыми.

Для двух независимых событий

.

Несколько событий называются попарно независимыми, если каждые два из них независимы.

События называются независимыми в совокупности, если вероятность каждого из них не меняется при наступлении других событий, одного или нескольких.

Вероятность произведения нескольких событий, независимых в совокупности, равна произведению их вероятностей:

События называются совместными, если они могут появиться одновременно в одном опыте.

Теорема сложения вероятностей двух совместных событий:

Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:

Теорема может быть обобщена на любое конечное число совместных событий. Например, для трех совместных событий

Событие называется противоположным событию А, если оно состоит в непоявлении события А.

Противоположные события должны одновременно удовлетворять двум соотношениям

1. - достоверное событие;

2. ; где - пустое множество.

Сумма вероятностей противоположных событий равна единице:

.

Вероятность появления хотя бы одного события.

Вероятность появления хотя бы одного события из событий то есть вероятность суммы независимых в совокупности событий вычисляется по формуле:

.

Если все события имеют одинаковую вероятность, равную , то вероятность появления хотя бы одного из этих событий определяется по формуле , где

Формула полной вероятности.

Формулы Байеса.

Если некоторое событие А может произойти с одним из n попарно несовместных событий (гипотез) образующих полную группу событий, то для определения вероятности этого события может быть использована формула полной вероятности

, где

- вероятность события ;

- условная вероятность события А, при каждой из гипотез

Для определения вероятности события при условии, что произошло событие А, используются формулы Байеса.

где ,

р(А) – полная вероятность события А.

Формулы Бернулли и Пуассона.

Если производятся испытания, при которых вероятность появления события А в каждом испытании не зависит от исходов других испытаний, то такие испытания называют независимыми относительно события А. Рассмотрим независимые испытания, в каждом из которых вероятность появления события одинакова.

Формула Бернулли.

Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна , событие наступит ровно m раз (безразлично, в какой последовательности), равна ,

где

вероятность того, что в n испытаниях событие наступит:

а) менее m раз; б) более m раз; в) не менее m раз; г) не более m раз, - находят соответственно по формулам:

1. 

2. 

3. 

4. 

При больших n и малых p вычисления по формуле Бернулли затруднены. В этих случаях обычно используется формула Пуассона

Дискретные случайные величины.

Случайной величиной называется величина, которая в результате опыта может принять любые заранее неизвестные значения. Различают дискретные и непрерывные случайные величины. Дискретной (прерывной) называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями. Число возможных значений дискретной случайной величины может быть конечным или бесконечным (счетным).

Законом распределения вероятностей (рядом распределения) дискретной случайной величины называется последовательность возможных значений случайной величины и соответствующих им вероятностей, причем

X			…
p			…

Ряд распределения можно задать графически, откладывая на горизонтальной оси значения X, а на вертикальной – соответствующие им значения вероятностей.

Графическое представление ряда распределения называется многоугольником распределения.

Для дискретной случайной величины можно ввести понятие функции распределения , которая равна вероятности случайного события, состоящего в том, что дискретная случайная величина X примет одно из возможных значений, меньших некоторого значения x, т.е.

.

Математическое ожидание и дисперсия.

Характеристикой среднего значения случайной величины служит математическое ожидание.

Математическим ожиданием дискретной случайной величины называют сумму произведений всех её возможных значений на их вероятности:

Если дискретная случайная величина принимает счетное множество возможных значений, то

причем математическое ожидание существует, если ряд в правой части равенства сходится абсолютно.

Математическое ожидание обладает следующими свойствами:

1. где С – произвольная постоянная величина.

2. если

- взаимно независимые случайные величины.

Несколько случайных величин называют взаимно независимыми, если законы распределения любого числа из них не зависят от того, какие возможные значения приняли остальные величины.

3. 

4. , где X – дискретная случайная величина;

n-число испытаний с биномиальным законом распределения;

Биномиальным называют закон распределения дискретной случайной величины X – числа появлений события в n независимых испытаниях, в каждом из которых вероятность появления события равна .

Характеристиками рассеяния возможных значений случайной

величины вокруг математического ожидания служат, в частности, дисперсия и среднее квадратичное отклонение.

Дисперсией случайной величины X называют математическое ожидание квадрата отклонения случайной величины от её математического ожидания:

.

Дисперсию удобно вычислять по формуле

Дисперсия обладает следующими свойствами.

1. где С – произвольная постоянная.

2. где - независимые случайные величины.

3. , где X –дискретная случайная величина с биномиальным законом распределения; n – число испытаний; - вероятность появления и вероятность непоявления события в одном испытании соответственно.

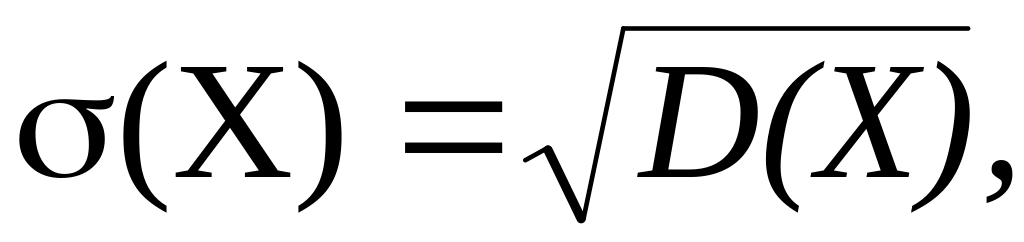4. где (X) – среднее квадратичное отклонение.

Непрерывные случайные величины.

Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка.

Функцией распределения называют функцию , определяющую для каждого значения x вероятность того, что случайная величина x примет значение, меньшее x, то есть

.

Функция распределения обладает следующими свойствами:

1. 

2. ,

3. ,

4. ,

5. .

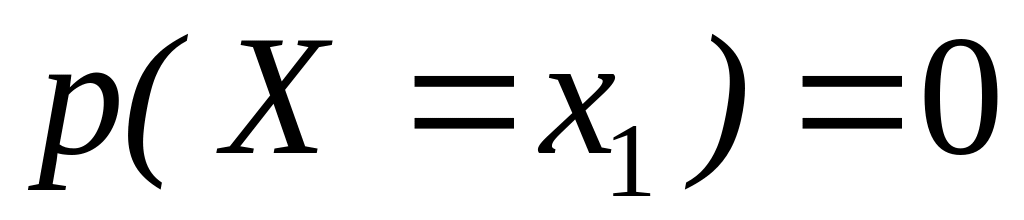Плотностью распределения вероятностей непрерывной случайной величины называют первую производную от функции распределения:

Вероятность того, что непрерывная случайная величина Х примет значение, принадлежащее интервалу (а; в), определяется равенством

.

Зная плотность распределения, можно найти функцию распределения

.

Плотность распределения обладает следующими свойствами:

1. ,

2. .

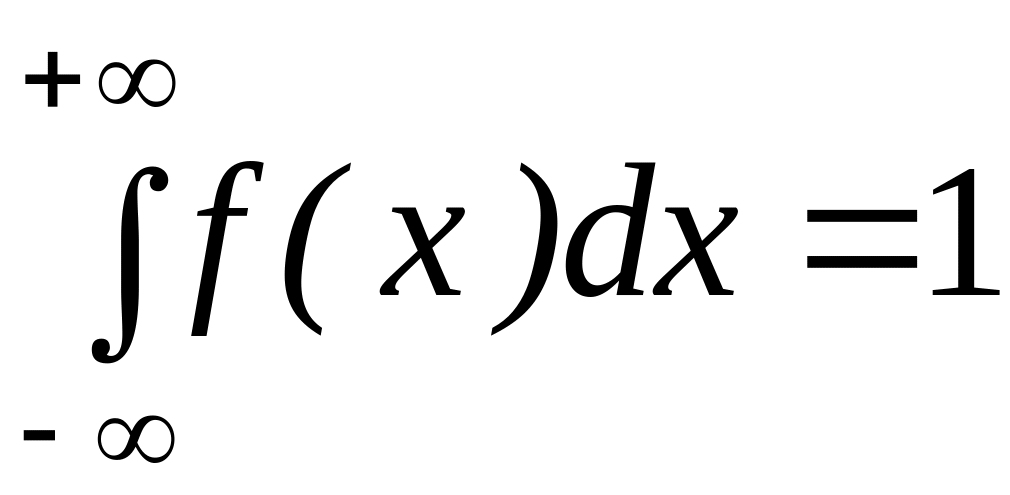Если все возможные значения случайной величины принадлежат интервалу (а; в), то .

Математическое ожидание и дисперсия.

Мода и медиана.

Средним значением или математическим ожиданием непрерывной случайной величины Х называется значение интеграла

, где - плотность вероятности.

Дисперсией непрерывной случайной величины Х называется значение интеграла

Для определения дисперсии может быть также использована формула .

Модой непрерывной случайной величины Х называется такое значение этой величины, плотность вероятности которого максимальна.

Медианой непрерывной случайной величины Х называется такое её значение, при котором выполняется равенство

.

Равномерное распределение.

Непрерывная случайная величина называется равномерно распределенной на отрезке [а; в], если её плотность вероятности имеет вид

.

Математическое ожидание и дисперсия равномерно распределенной случайной величины определяются выражениями

.

Показательное распределение.

Распределение непрерывной случайной величины Х называется показательным (экспоненциальным), если плотность вероятности этой величины описывается функцией

где λ – положительное число.

Соответственно, функция распределения вероятностей имеет вид

Математическое ожидание и дисперсия показательного распределения соответственно равны:

Нормальное распределение.

Случайная величина Х распределена по нормальному закону, если её функция плотности распределения вероятностей имеет вид

,

где - математическое ожидание;

– среднее квадратичное отклонение.

Вероятность попадания случайной величины в интервал (а; в) находится по формуле

где - функция Лапласа.

Значения функции Лапласа для различных значений Z приведены в Приложении.

Функция Лапласа нечетная, то есть

Вероятность того, что абсолютная величина отклонения меньше положительного числа ε, .

Мода и медиана нормального распределения соответственно равны:

Законы распределения двумерной случайной величины.

Двумерной называют величину (X; У), возможные значения которой есть пары чисел (x; у). Случайные величины X и У, рассматриваемые одновременно, образуют систему двух случайных величин.

Функцией распределения вероятностей двумерной случайной величины называют функцию , определяющую для каждой пары чисел (x; у) вероятность того, что Х примет значение, меньшее х, и при этом У примет значение, меньшее у:

Для дискретной случайной величины распределение может быть задано в виде таблицы распределения, в которой каждой паре значений ставится в соответствие вероятность появления этой пары

.

Плотностью совместного распределения вероятностей непрерывной двумерной случайной величины называют вторую смешанную производную от функции распределения:

.

Функция распределения вероятностей непрерывной случайной величины выражается через двумерную плотность вероятности по формуле

.

Вероятность совместного появления пары дискретных случайных величин можно записать в виде

где - условные вероятности.

Для непрерывных случайных величин плотность вероятности записывается в виде

Числовые характеристики системы двух случайных величин.

Среди числовых характеристик двумерной случайной величины важнейшими являются условное математическое ожидание и ковариация.

Условным математическим ожиданием дискретной случайной величины У при Х=х называют сумму произведений возможных значений У на их условные вероятности

Для непрерывных случайных величин условное математическое ожидание определяется интегралом:

Условное математическое ожидание называется также регрессией величины У на Х.

Аналогично определяется регрессия Х на У:

для дискретной случайной величины

;

для непрерывной случайной величины

.

Ковариацией или корреляционным моментом

случайных величин Х и У называется математическое ожидание произведения отклонений этих величин от их математических ожиданий:

Коэффициентом корреляции случайных величин Х и У называется отношение ковариации к произведению средних квадратичных отклонений этих величин:

Линейной средней квадратической регрессией У на Х называется функция вида

где

С примерами решения задач по теории вероятностей Вы можете познакомиться в книге: «Методические указания к проведению практических занятий по теории вероятностей». Челябинск: ЧИ МГУК, 1999. - 144с.