9 Класс (11-летний срок обучения)

10 Класс (12-летний срок обучения)

1. Преобразуем исходное выражение: Это число будет рациональным, когда является полным кубом рационального числа. Наименьшим натуральным значением k является

.

(7 баллов)

6. Пусть данное уравнение имеет решение , то тогда имеем , которое равносильно уравнению . Из последнего уравнения следует, что число четное. Значит, делится на 4. В итоге получаем, что в равенстве левая часть делится на 4, а правая только на 1 – противоречие. Значит, уравнение решений в целых числах не имеет.

(6 баллов)

2. Пусть открытка представляла собой прямоугольник . При разрезании ее на два прямоугольника одинаковой площади могли получиться либо прямоугольники , либо прямоугольники . Для определенности будем считать, что Петя получил прямоугольники ; периметр одного такого прямоугольника равен .

Прямоугольник, оставшийся у Васи после первого разрезания, не мог иметь размеры . (В самом деле, если бы он был равен прямоугольнику, оставшемуся у Пети, то после второго разрезания у Васи остался бы либо прямоугольник , либо прямоугольник ; в обоих случаях периметр оказался бы меньше, чем ). Следовательно, после первого разрезания Вася имел прямоугольник . При втором разрезании одна из сторон этого прямоугольника уменьшилась вдвое, и, поскольку периметр прямоугольника меньше, чем , то в итоге у Васи мог остаться только прямоугольник периметра .

Из равенства находим искомое отношение .

(10 баллов)

3. При указанной операции не меняется четность количества минусов. Поэтому последний знак – «+», если было написано четное число, и «–», если – нечетное.

(4 балла)

4. Обозначим угол за (см. рисунок), и пусть 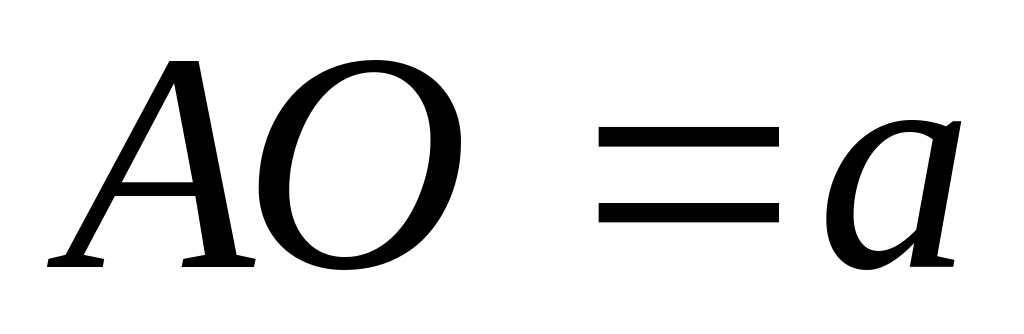, 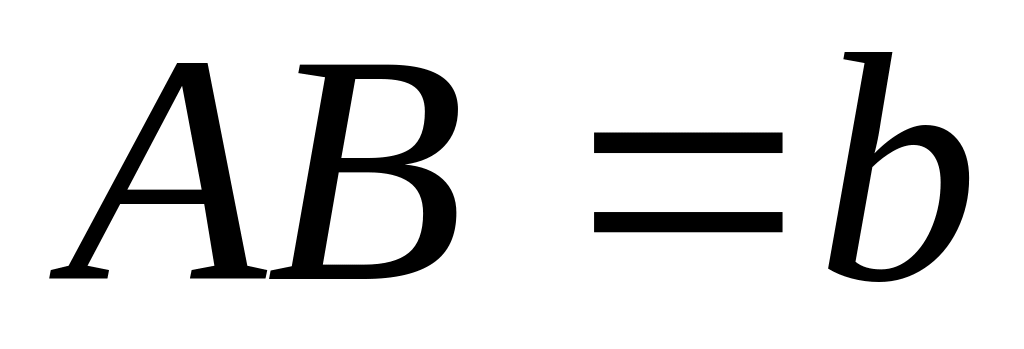. Тогда найдем стороны треугольника , применяя теорему косинусов к треугольникам , , 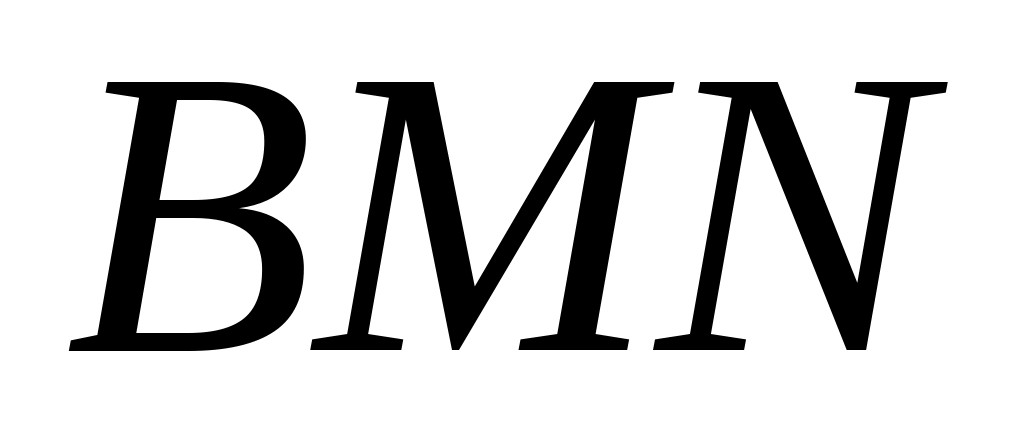: . Так как квадраты сторон треугольника равны, то и сами стороны будут равны, т.е. треугольник будет равносторонним.

N

M B C

A D

(8 баллов)

ОТВЕТЫ, УКАЗАНИЯ, РЕШЕНИЯ

10 Класс (11-летний срок обучения)

1. Обозначим число килограммов краски, которое надо купить, за N. Тогда N будет иметь вид , или .

Рассмотрим числа вида . Тогда надо брать банок по 3 кг.

Рассмотрим числа вида . Минимальное число килограммов краски этого вида будет 10 кг. Тогда 10 = 5 + 5. Если , то берем 2 банки краски по 5 кг и банки краски по 3 кг .

Рассмотрим числа вида . Минимальное число такого вида, большее 7, будет 8 = 3 + 5. Если же , то берем 1 банку по 5 кг и банку по 3 кг .

(8 баллов)

2. Пусть Б – количество блондинов, Г – количество голубоглазых, М – общее количество людей, ГБ – количество голубоглазых блондинов. По условию 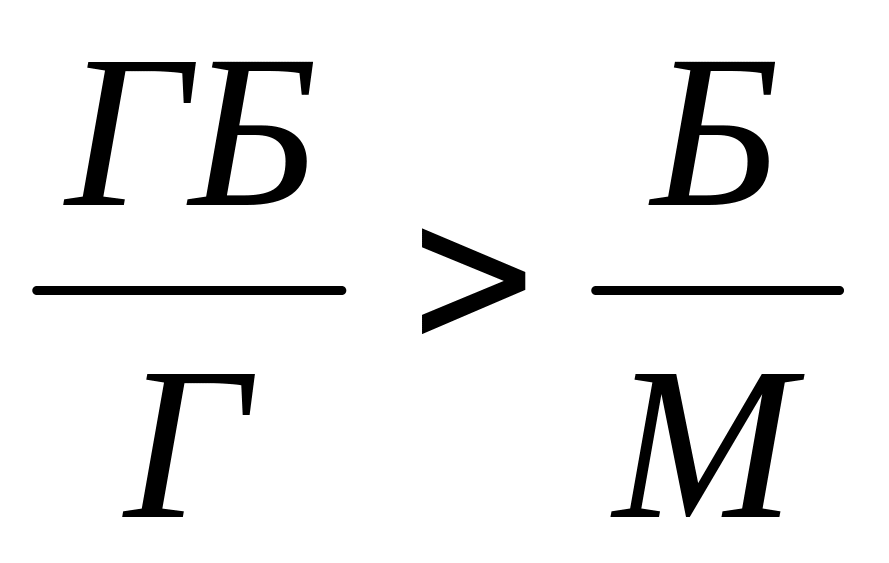. Но тогда .

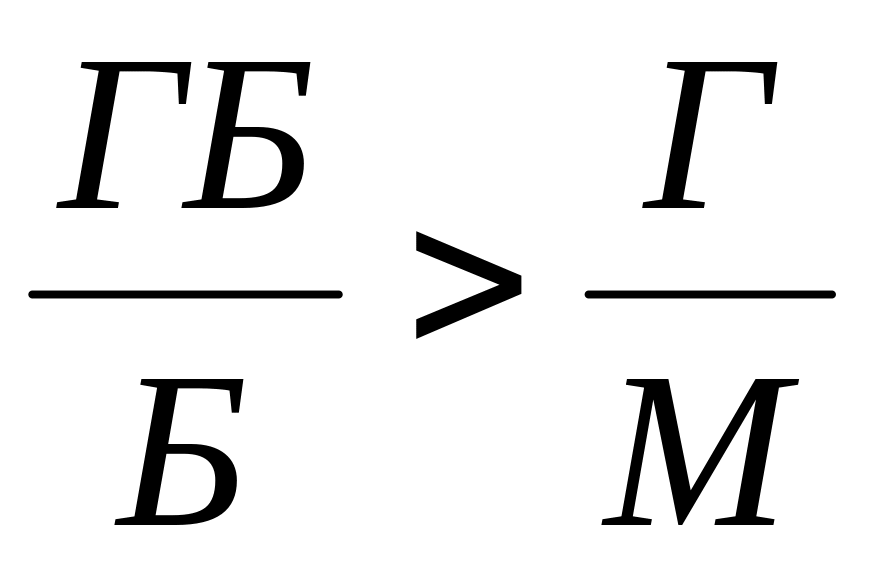Ответ: Доля голубоглазых среди блондинов больше.

(6 баллов)

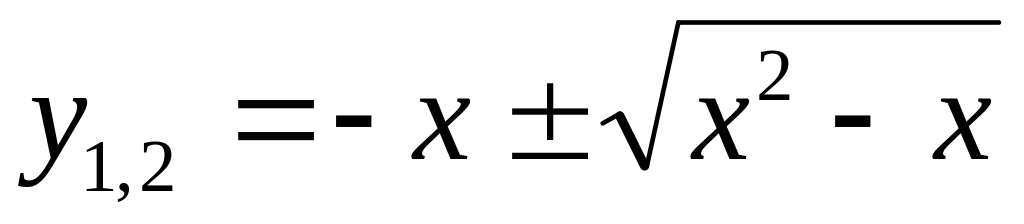3. В памяти есть число . Складывая его с самим собой, получаем . Сравниваем эти числа ( и ). Если они равны, то , в противном случае найдем корни уравнения , т.е. . Если , то , в противном случае .

(9 баллов)

4. Данная фигура существует. Ее можно получить из двух равных треугольников и , приложенных друг к другу по стороне BC под некоторым углом.

(5 баллов)

5. Обозначим радиус данного круга за . Тогда радиус искомого круга . Его можно найти как длину гипотенузы прямоугольного треугольника с катетами и .

(7 баллов)

ОТВЕТЫ, УКАЗАНИЯ, РЕШЕНИЯ