4.2. Методика проведения группировки

Проведение группировки предполагает решение следующих задач:

1) выбор группировочного признака

2) определение числа групп и величины интервалов

3) описание комбинации группировочных признаков (при наличии нескольких признаков)

4) установление показателей, которыми должны характе­ризоваться группы

Основной целью типологической группировки является выделение качественно однородных совокупностей и исследование структуры совокупности как таковой.

Существуют 2 способа формирования типологических групп:

1) способ последовательных разбиений, заключающийся в формировании групп, все объекты которых имеют одинаковые значения классификационных признаков

2) способ многомерной классификации, когда объекты, образующие группы, могут иметь различные значения класси­фикационных признаков.

Первый способ основан на методе комбинационной группировки, при которой формирование групп производится путем последовательного разбиения сначала всей совокупности по одному признаку, затем полученных частей – по другому и так далее (причем строго соблюдается принцип иерархии групп), а также на многошаговом методе последовательных разбиений совокупности.

Способ многомерной классификации означает, что группы формируются на основе сходства объектов одновременно по большому числу признаков.

При использовании методов комбинационной группировки классификация осуществляется путем последовательного логического деления совокупности по отдельным признакам.

При этом предусматривается следующая очередность этапов:

1) выделение типов

2) выбор группировочного признака (признаков)

3) определение числа групп и величины интервалов

4) сведение выделенных групп в типы

5) характеристика типов с помощью системы показателей

Выделение типов производится с помощью теоретического качественного анализа. Предварительно намечают столько типов, сколько их может быть в данной совокупности теоретически (хотя фактически возможно меньшее их число).

При выборе группировочного признака необходимо учитывать 2 условия:

1) типологическая группировка должна выполняться только по существенным признакам

Теоретически можно охватить все существенные признаки, однако при таком подходе получается излишнее дробление совокупности. Группы оказываются малы по объему и не пригодны для статистического анализа. Поэтому рекомендуется проводить группировку по двум-трем главным признакам, взятым в комбинации.

2) при необходимости для характеристики разных типов выбираются различные признаки (осуществляется специализация признака)

На различных этапах формирования типологической группировки число групп неодинаково. По её завершении оно соответствует фактическому числу выделенных типов.

В случае количественного группировочного признака необходимо определять величину интервалов.

Интервалы задают критические точки перехода одного качества в другое. При построении типологической группировки интервалы должны быть неравными и специализированными.

Структурная группировка применяется для изучения строения совокупности, характеристики ее структуры и структурных сдвигов.

Наличие и количественные соотношения различных групп представляют собой важную черту совокупности. Анализ структуры совокупности позволяет сделать определенные выводы, важные для практической деятельности.

Структурные группировки строятся либо на основе ранее проведенной типологической группировки, либо на основе первичных данных. Проведение структурной группировки по первичной статистической информации предполагает решение таких методологических вопросов, как:

1) выбор группировочного признака

2) определение числа групп и величины интервала

Здесь необходимо учитывать несколько условий:

а) число групп определяется колебанием группировочного признака: чем значительнее вариация признака, тем больше при прочих равных условиях должно быть групп

б) число групп должно отражать реальную структуру изучаемой совокупности

в) не допускается выделение пустых групп

Если проблема пустых групп все же возникает, при проведении структурных группировок используют неравные интервалы.

Для нахождения оптимального числа групп используется формула Стерджесса

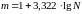
где N – количество элементов совокупности.

В случае равных интервалов величину интервала можно определить по формуле:

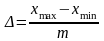
где m – количество групп (заданное заранее или рассчитанное по формуле Стерджесса), 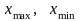– максимальное и минимальное значения группировочного признака

3) определение системы показателей для характеристики групп.

Обязательным показателем является численность групп. Он может быть представлен либо частотой (количеством единиц в каждой группе), либо частотностью (удельным весом каждой группы).

Одним из видов структурной группировки является ряд распределения. Элементами распределения являются варианты (названия или количественные выражения группировочного признака) и частота (численность единиц, относящихся к каждой группе).

Количественные признаки могут выражаться дискретными или непрерывными величинами, соответственно, и вариационный ряд будет либо дискретным, либо интервальным (непрерывным в пределах интервала).

При построении вариационного ряда непрерывного признака невозможно указать абсолютно точное значение варианта, поэтому совокупность распределяется по интервалам его значений. Интервалы можно брать как равные, так и неравные. Для каждого из них указывается частота или частотность (абсолютное или относительное число единиц, у которых значение признака находится внутри данного интервала).

Первый и последний интервалы рядов можно брать открытыми. Использование открытых интервалов удобно, когда в совокупностях встречается незначительное число единиц с очень малыми или очень большими значениями вариантов, резко отличающимися от всех остальных значений.

Если построен ряд с равными интервалами, то частоты дают представление о том, как заполнен единицами совокупности тот или иной интервал. При сравнении частот ряда с неравными интервалами для характеристики их заполненности вычисляется плотность распределения.

Средняя плотность в интервале – частное от деления частоты или частотности на величину интервала: в первом случае получается абсолютная, во втором – относительная плотность распределения.

Средняя плотность показывает, сколько единиц (или сколько процентов единиц) совокупности приходится на единицу изменения варианта.

Для характеристики распределения используют также накопленные частоты. Если вместо абсолютных частот взять частотности, то аналогично получим накопленные частотности.

Накопленная частота (частотность) для данной группы (дискретного значения или верхней границы данного интервала) – сумма частот (частотностей) всех предшествующих групп, включая данную.

Накопленная частота показывает, какое число единиц имеет значение признака, не большее данного значения дискретной группы или верхней границы интервала.

Частота, частотность, плотность и накопленная частота вариационного ряда – различные функции от величины варианта.

Зависимость частот (точнее, плотностей распределения) от значений изучаемого признака может быть представлена в виде некоторой функции, изображаемой графически кривой определенного вида.

Любое реальное распределение можно также изобразить схематически в виде некоторой кривой, воспроизводящей основные особенности данного распределения. В зависимости от вида кривых, изображающих распределение, выделяют несколько основных типов распределений.

Прежде всего распределения по виду их графического изображения можно разделить на одновершинные и многовершинные. К одновершинным относятся те, в которых один, обычно центральный, вариант имеет наибольшую частоту (точнее, наибольшую плотность распре­деления), частоты же остальных вариантов убывают по мере удаления от центрального.

Если частоты убывают одинаково и справа и слева от центрального значения, то такие распределения называются симметричными. Если частоты убывают слева и справа от центра распределения с разной скоростью, то такие распределения называют асимметричными, выделяя при этом распределения, растянутые вправо и влево.

Степень асимметрии может быть различной: от совершенно незначительной до крайней, при которой наибольшая частота относится к одному из крайних значений вариантов (максимальному или минимальному).

Различные виды распределений представлены на рисунке.

1) одновершинное симметричное

2) одновершинное умеренно асимметричное:

а) с левосторонней асимметрией

б) с правосторонней асимметрией

3) крайне асимметричное

4) многовершинное

Идеальное симметричное распределение крайне редко встречается на практике (практически близки к нему распределения мужчин и женщин по весу или росту при достаточно большом количестве людей, включенных в совокупность).

Основная масса распределений, с которыми приходится иметь дело экономисту – асимметричные распределения с разной степенью асимметрии.

Многовершинные распределения имеют несколько центров (несколько максимумов частот).

Многовершинность распределения часто является свидетельством того, что совокупность состоит из неоднородных (с точки зрения изучаемого признака) единиц.

Поэтому при выявлении у распределения нескольких максимумов частоты, нужно проверить, можно ли считать однородными единицы совокупности.

В практической деятельности очень важно фактическое распределение (структуру совокупности) привести к известному теоретическому. Обычно в экономических расчетах аппроксимируют к следующим теоретическим распределениям:

1) нормальное

2) равномерное

3) показательное

4) распределение Пуассона (для дискретных распределений)

При этом решается задача проверки соответствия выбранной кривой для представления фактической структуры. Необходимо выяснить, действительно ли различия между теоретической и эмпирической кривой распределения настолько малы, что их можно считать случайными, а не закономерными.

Наиболее известный метод проверки соответствия фактического и теоретического рядов распределения – применение критерия согласия Пирсона.

Аналитическая (факторная) группировка предназначена для установления тесноты связи между взаимодействующими признаками – факторными и результативным. Она позволяет выявить наличие и направление связи, а также измерить ее тесноту и силу.

Методологическими вопросами построения факторной группировки являются выбор группировочного признака, определение числа групп и величины интервала, выбор системы показателей для характеристики групп.

В качестве группировочного чаще всего принимают факторный признак, выделенный на основе априорного анализа. Интервалы в аналитической группировке берутся преимущественно равные или равнонаполненные (группы с приблизительно одинаковой частотой). Величина интервала рассчитывается так же, как при построении структурной группировки. Среди показателей групп обязательным является среднее значение результативного показателя по каждой группе. Теснота связи оценивается сравнением вариации этих средних значений с вариацией резуль­тативного показателя.