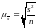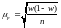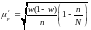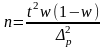- •Тема 1. Предмет, методЫ и задачи статистики.
- •Тема 2. Статистические признаки и показатели.
- •Тема 3. Статистическое наблюдение
- •3.1. Формы, виды и способы статистического наблюдения
- •3.2. Организация статистического наблюдения
- •3.3. Контроль результатов статистического наблюдения
- •4. Статистическая сводка и группировка
- •4.1. Основные понятия и определения
- •4.2. Методика проведения группировки
- •5. Статистические таблицы и графики
- •6. Статистические величины.
- •7. Статистическое изучение вариации
- •7.1. Показатели вариации
- •7.2. Вариация альтернативного признака.
- •7.3. Правило сложения дисперсий
- •8. Выборочное наблюдение
- •8.1. Простая случайная выборка
- •8.2. ТипичесКая выборка
- •8.3. Серийная выборка
- •8.4. Механическая выборка
- •8.5. Метод моментных наблюдений
- •8.6. Малые выборки
- •9. Ряды динамики
- •9.1. Основные понятия
- •9.2. Показатели интенсивности ряда динамики
- •9.3. Выявление и характеристика основной тенденции ряда динамики
- •9.4. Статистическое изучение сезонных колебаний
- •10. Индексный метод в статистике
- •10. 1. Основные понятия
- •10.2. Индексы количественных показателей
- •10.3. Индексы качественных показателей
- •10.4. Цепные и базисные индексы
- •10.5. Индексы средних величин
- •10.6. Использование индексов
- •10.7. Примеры индексного анализа
- •11. Статистическое изучение взаимосвязей.
- •11.1. Сущность корреляционной связи
- •11.2. Корреляционно-регрессионный метод анализа
- •12. Статистика населения
- •12.1. Основные показатели численности населения и методика их расчета
- •12.2. Анализ естественного движения и миграции населения
- •9. Статистика основного капитала
- •9.1. Основные фонды
- •9.2. Показатели наличия и структуры основных производственных фондов
- •9.3. Показатели состояния и движения основных производственных фондов
- •9.4. Показатели использования основных производственных фондов
- •9.5. Состав, наличие и использование парка оборудования
- •10. Статистика оборотного капитала
- •10.1. Оборотный капитал и запасы материальных ценностей
- •10.2. Показатели объема и структуры запасов материальных ценностей
- •10.3. Показатели использования запасов материальных ценностей
- •11. Показатели статистики продукции
- •11.1. Показатели промышленной продукции
- •11.2. Показатели продукции капитального строительства
- •11.3. Основные показатели эффективности производства и
- •12. Статистика труда
- •12.1. Статистика занятости населения
- •12.2. Показатели численности и состава персонала предприятия.
- •10.4. Производительность труда. Основные показатели и методы расчета
- •13. Себестоимость продукции и структура затрат на производство
- •13.1. Показатели себестоимости продукции
- •13.2. Анализ структуры затрат на производство
- •14. Статистика финансовой деятельности предприятия
- •14.1. Показатели прибыли и рентабельности
- •14.2. Показатели финансового состояния предприятия и методика их расчета
- •14.3. Факторный анализ прибыли от реализации товаров и услуг
- •14.4. Анализ факторов рентабельности
- •15. Статистическое изучение брака и статистика качества продукции.
- •15.1. Виды брака
- •15.2. Оплата труда при изготовлении брака
- •15.3. Возмещение ущерба от изготовления брака
- •15.4. Определение потерь от брака
- •16. Статистика качества продукции
- •16.1. Система показателей качества продукции
- •16.2. Конкурентоспособность продукции, ее сущность и методы определения
- •16.3. Факторы, влияющие на качество продукции
- •16.4. Система управления качеством продукции на предприятии
- •16.5. Экономическая эффективность повышения качества продукции
- •1. Система показателей уровня жизни населения
- •2. Показатели доходов населения
- •3. Показатели расходов и потребления населением товаров и услуг
- •4. Показатели социальной дифференциации населения
8.1. Простая случайная выборка
Простая случайная выборка предполагает отбор единиц в выборочную совокупность непосредственно из всей массы единиц генеральной совокупности в форме случайного отбора.
При этом каждой единице генеральной совокупности обеспечивается одинаковая вероятность быть выбранной. Случайный отбор осуществляется путём применения жеребьевки (лотереи) или использования таблиц случайных чисел.
Случайный отбор может быть повторным и бесповторным.
Выборочная средняя и выборочная доля являются величинами, которые могут принимать различные значения в зависимости от того, какие единицы совокупности попали в выборку.
Следовательно, ошибка выборки также является случайной величиной и может принимать различные значения.
Средняя ошибка выборки представляет собой среднее значение из всех возможных ошибок.
Численное значение средней ошибки выборки определяется по формулам:
Вид отбора
Формула ошибки |
Повторный |
Бесповторный |
Для средней |
|
|
Для доли |
|
|
Предельная ошибка выборки связана с гарантирующим её уровнем вероятности. Уровень вероятности задаётся через коэффициент доверия t и наоборот. Значения коэффициента t берутся из таблицы значений функции Лапласа.
t |
1 |
1,96 |
2 |
2,58 |
3 |
= (t) |
0,683 |
0,950 |
0,954 |
0,990 |
0,997 |
Предельная ошибка связана со средней ошибкой по формулам:


Используя предельную ошибку выборки, можно решать следующие задачи:
1. Найти пределы генеральной характеристики с заданной степенью надежности (доверительной вероятностью) на основе показателей, полученных по данным выборки.
Доверительный интервал для генеральной средней определяется выражением

Доверительный интервал для генеральной доли
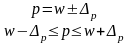
Увеличение степени достоверности результатов требует большего значения t и увеличивает предельную ошибку. Уменьшение степени достоверности результатов приводит к меньшей предельной ошибке.
2. Определение доверительной вероятности того, что генеральная характеристика отличается от выборочного показателя не более чем на заданную величину.
Доверительная
вероятность является функцией параметра
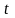 .
Значение этого параметра можно вычислить
по заданной выборке и известной предельной
ошибке. По величине t
определяется доверительная вероятность
как значение функции Лапласа.
.
Значение этого параметра можно вычислить
по заданной выборке и известной предельной
ошибке. По величине t
определяется доверительная вероятность
как значение функции Лапласа.
3. Определение необходимого объема выборки, который с практической вероятностью обеспечивает заданную точность выборки.
Формулы численности случайной выборки зависят от вида отбора:
Вид отбора
Численность выборки |
Повторный |
Бесповторный |
Для средней |
|
|
Для доли |
|
|
Дисперсия s2 может быть получена следующим образом:
1) взята из предыдущих исследований
2) если известен размах вариации, то ≈ R / 6
3) если известно среднее значение, то ≈ / 3
Если доля w неизвестна, то в расчётах используется максимальная величина дисперсии доли, равная 0,25.