Задача №10

Величина t розподілена за експонентною характеристикою . Визначити ймовірність того, що величина t потрапить у період .

Розв’язання

Згідно з показниковим законом розподілу, ймовірність попадання у даний інтервал дорівнює

Відповідь: ймовірність попадання величини t в даний інтервал дорівнює 0,508.

Задача №11

У результаті спостережень приведена таблиця у вигляді статистичного ряду середньомісячних спусків води із водосховища та відповідно їм вироблення електроенергії на ГЕС.

N	1	2	3	4	5	6	7	8	9	10	11	12
Q/Qmax	0,5	0,4	0,8	1	1	0,9	0,9	0,85	0,65	0,6	0,55	0,5
N/Nmax	0,4	0,35	0,7	1	0,95	0,85	0,8	0,75	0,55	0,45	0,45	0,4

Обчислити статистичні характеристики двомірного випадкового вектора та записати одне із рівнянь регресії його компонент.

Розв’язання

Математичне сподівання для кожного елемента відповідно

Дисперсія

Середнє квадратичне відхилення

Коефіцієнт коваріації

Запишемо рівняння регресії у одному випадку

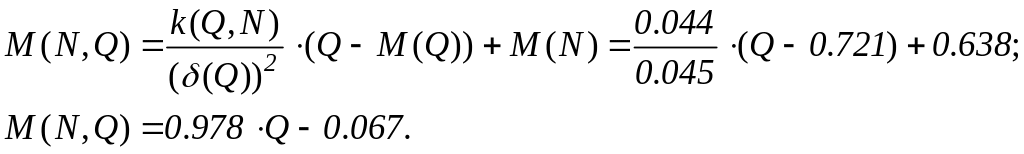
Відповідь:

та рівняння регресії

Задача №12

За результатам показів вольтметра, встановленого на шина підстанції 110/10 кВ, було побудовано наступний статистичний ряд відхилення напруги на шина 10 кВ:

U,%	-4 -3	-3 -2	-2 -1	-1 0	0 1	1 2	2 3	3 4
Mi	23	25	27	26	22	28	25	24

1. Обчислити статистичне середнє квадратичне відхилення

2. Побудувати статистичну функцію розподілу.

3. Побудувати гістограму відхилення U

4. Повести аналітичну апроксимацію .

5. Виконати перевірку гіпотези по критерію

Розв’язання

1. Загальна кількість зафіксованих відхилень 200, отже, запишемо ряд статистичних ймовірностей.

Mi	23	25	27	26	22	28	25	24
Pk	0,115	0,125	0,135	0,13	0,11	0,14	0,125	0,12

Математичне сподівання обчислюється, як сума добутку середнього значення Х, наприклад -3,5, на відповідну статистичну ймовірність, тобто:

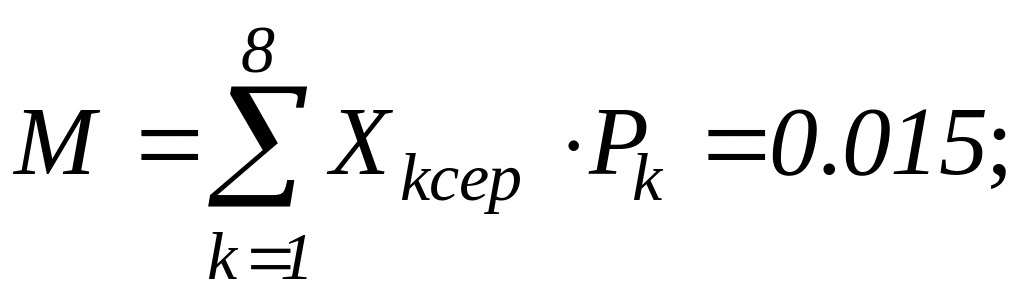
Дисперсія обчислюється як сума добутку квадрата різниці середнього значення та математичного сподівання на відповідну ймовірність, тобто:

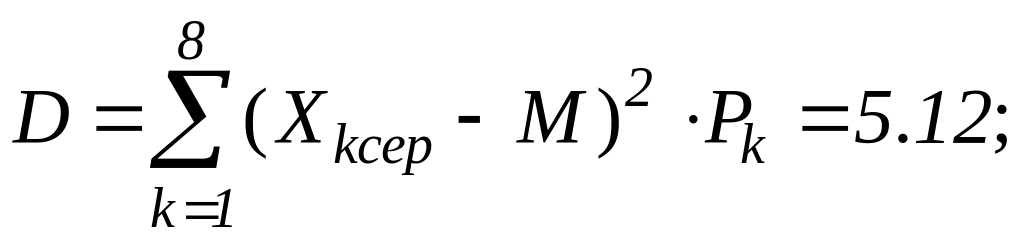
Таким чином, стандартне відхилення по модулю

2. Для побудови статистичної функції розподілу обчислимо її складові за наступним алгоритмом:

Маємо:

X	X1	X2	X3	X4	X5	X6	X7	X8	X9
F(X)	0	0,115	0,24	0,375	0,505	0,615	0,755	0,88	1

Побудуємо графік

3. Зобразимо гістограму розподілу відхилення напруги

4. Висуваємо припущення, що даний розподіл підвладний нормальному розподілу.

5. Для аналітичного опису даної функції запишемо:

де , а

Накладемо аналітичний розподіл на статистичні дані

6. Для перевірки висунутої гіпотези використаємо критерій

Обчислимо

Використовуючи дане значення та значення числа вільних зв’язків де r – кількість інтервалів, s – кількість параметрів висунутого аналітичного розподілу. У нашому випадку k=5. Отже ступінь значимості по таблиці 0,95. Це говорить нам про те, що висунута гіпотеза із ймовірністю 0,95 описує наш розподіл відхилення напруги на шинах 10 кВ.