Типові задачі по курсу «теорія надійності енергосистем».

Задача №1

Ділянка енергосистеми має наступну схему

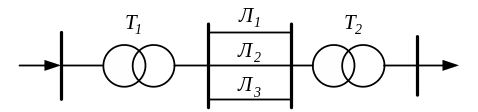
Ймовірність відмови елементів, відповідно:

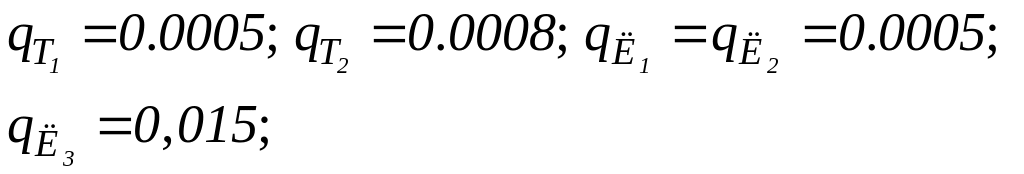
Визначити ймовірність безперервного енергопостачання споживачів, що живляться від підстанції з трансформатором .

Розв’язання

Використовуючи теорему про суму ймовірностей для даного випадку маємо:

Подія А – відмова першого трансформатора.

Подія В – відмова усіх паралельних ліній електропередачі.

Подія С – відмова другого трансформатора.

Подія А+В+С – припинення енергопостачання споживачів із-за вище приведених випадків.

Отже:

Відповідь: надійність 0,9987.

Задача №2

Статистична ймовірність пошкодження кожного ланцюга двох ланцюгової лінії електропередач дорівнює

Лінія забезпечує 75% резерву енергопостачання. Перший ланцюг може забезпечити 75% енергопостачання споживачів. Розглядаючи пошкодження ланцюгів ЛЕП, як незалежні події визначити ймовірність повної втрати енергопостачання, а також 25% дефіциту потужності у споживачів.

Розв’язання

Подія – відмова першого ланцюга лінії.

Подія – відмова другого ланцюга лінії.

Подія А – припинення енергопостачання, або його дефіцит.

Відповідь: ймовірність припинення та дефіциту постачання електроенергії у споживачів відповідно

Задача №3

Дві електростанції працюють на спільне навантаження. Повне енергозабезпечення можливе лише при одночасній роботі двох електростанцій. Ймовірність безвідмовної роботи за час для першої електростанції дорівнює 0,96, для другої – 0,94. У системі за даний час мало місце одноразове припинення енергопостачання. Визначити ймовірність того, що припинення викликане відмовою першої електростанції.

Розв’язання

Оскільки у задачі йдеться про припинення енергопостачання із-за відмови першої електростанції (події несумісні, та складають повну групу подій) використаємо формулу Бейеса.

де – повна ймовірність.

Подія – обидві електростанції працюють.

Подія – відмовила перша електростанція.

Подія – відмовила друга електростанція.

Подія – відмовили обидві електростанції.

Відповідно ймовірності даних подій.

Відповідь: ймовірність припинення енергопостачання споживачів із-за відмови першої електростанції дорівнює 0,385.

Задача №4

Статистична ймовірність пошкодження ізоляції трансформатора за нормального режиму мережі із малим током замикання на землю дорівнює

При замикані однієї фази мережі на землю ймовірність пошкодження збільшується до Як показують спостереження, робота з заземленою фазою мережі має протяжність 100 годин в рік.

Знайти ймовірність пошкодження трансформатора.

Розв’язання

Подія А – пошкодження трансформатора, яка можлива у вдвох випадках.

Подія – пошкодження трансформатора у період заземленої фази.

Подія – пошкодження трансформатора у решту часу.

Використовуючи формулу для повної ймовірності, маємо:

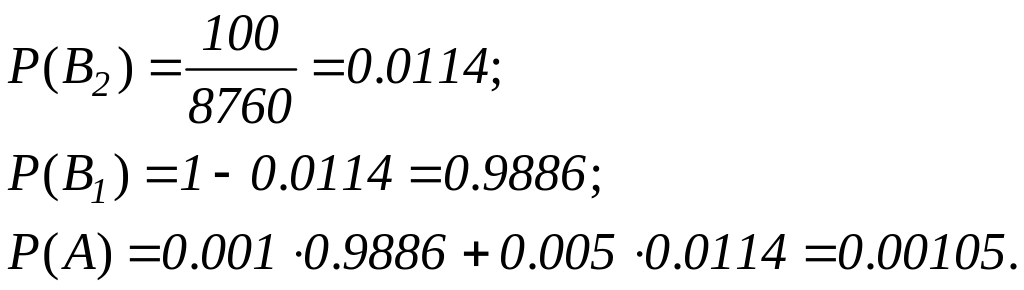
Відповідь: ймовірність пошкодження трансформатора за рік становить 0,00105.