
- •2.Сила Лоренца. Движение заряженной частицы в магнитном поле.
- •3.Закон Ампера.
- •4.Контур с током в магнитном поле.
- •5.Закон полного тока для магнитного поля в вакууме. Применение теоремы о циркуляции вектора в.
- •6.Работа перемещения проводника с током в постоянном магнитном поле.
- •7.Магнитные моменты электронов и атомов. Диа- и парамагнетизм.
- •10.Энегрия магнитного поля.
- •11.Первое уравнение Максвелла. Ток смещения. Второе уравнение Максвелла. Теорема Гаусса для магнитного поля. Третье и четвертое уравнения Максвелла.
1.Закон Био-Савара-Лапласа. Расчет магнитных полей на основе закона Био-Савара-Лапласа.

Рассмотрим элемент проводника с током

Заряды движутся в одном направлении с примерно одинаковой скоростью
 -объемная
плотность заряда
-объемная
плотность заряда
dl - длина элемента проводника
 ,
e-заряд
электрона, n-
концентрация
,
e-заряд
электрона, n-
концентрация
 Закон
БСЛ для объемного проводника с током
Закон
БСЛ для объемного проводника с током




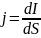

Вокруг проводника с током линии магнитной индукции представляют собой концентрические окружности, центры которых лежат на самом проводнике.

Магнитное поле прямого тока


для
бесконечно длинного проводника:

Линия будет окольцовывать проводник согласно правому винту.
Магнитное поле кругового тока.

Если построить все dB из каждого dl, то они будут представлять собой конический веер.








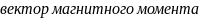


2.Сила Лоренца. Движение заряженной частицы в магнитном поле.
Сила
Лоренца перпендикулярна
 и
и
 .
.
Fл всегда перпендикулярна вектору скорости, поэтому она не меняет скорости по модулю, а лишь по направлению. По этой же причине Fл не совершает работы. Поскольку Fл перпенд. в. скорости частицы она может сообщить ей только нормальное ускорение.







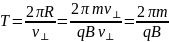
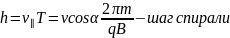
3.Закон Ампера.
На проводник с током, находящимся в м.п., действует сила Ампера, приложенная к малому элементу проводника с током = геометрической сумме сил, которые действуют со стороны м.п. на движущиеся в проводнике носители тока.
В
каждом элементе
 содержится N
носителей тока.
содержится N
носителей тока.








4.Контур с током в магнитном поле.

Рассмотрим силы действующие на 1-4 и 2-3.

1-2 и 3-4

Силы 1 и 3 рамку растягивают.
Силы 2 и 4 задают вращающий момент.



Неоднородное поле

1-устойчивое равновесия, растягивается и движется
2-неустойчивое равновесие, сжимается, выталкивая в сторону слабого поля
Сила Ампера действующая на замкнутый проводник с током со стороны м.п.как внешнего, так и собственного поля в проводнике, вызывают деформацию проводника, поэтому в проводниках, по которым текут очень Б токи и которые находятся в м.п., возникают столь значительные внутренние напряжения, что они могут угрожать прочности проводника.
В неоднородном м.п. действие силы Ампера сводится не только к результирующему моменту, в этом случаи на контур действует еще и результирующая сила. Под действием этой силы незакрепленный контур с током втягивается в область более сильного поля если угол м/у pm и В острый.
Если угол тупой, то контур с током выталкивается в область более слабого поля, поворачиваясь под действием момента силы Ампера так, что угол острым и затем втягивается в область более сильного поля.
Поведение контура с током в м.п. похоже на поведение диполя в эл.п.
Теорема Остроградского-Гауса.
Магнитный поток.
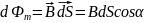



Эта формула является выражением того, что в природе нет магнитных зарядов, т.е. источников м.п., на которых начинались бы или заканчивались линии магнитной индукции.
Линия проходит так чтобы в каждой т. вектора магнитной индукции совпадал с касательной этой линии.
Линии магнитной индукции не могут пересекаться, густота линий характеризует интенсивность данного поля, что количественно выражается через величину магнитного потока.
5.Закон полного тока для магнитного поля в вакууме. Применение теоремы о циркуляции вектора в.
Циркуляция магнитной индукции поля в вакууме вдоль произвольно замкнутого контура, мысленно проведенного в магнитном поле = произведению магнитной постоянной на алгебраич. сумму токов, охватываемых этим контуром, т.е. на электрический ток ч/з поверхность, натянутую на этот контур.

Применение теоремы о циркуляции вектора В.
Рассчитаем с помощью закона полного тока магнитное поле.

1:

3: , т.к. токи О и О в сумме дадут 0
W на каждый ток уходящий от нас есть ток приходящий на нас.
L2: R1<r<R2
2:

Количество пронизывающих токов = количеству витков.

n-плотность намотки- число витков на единицу длины
Если неограниченно увеличивать R средней линии сохраняя неизменными, то в пределе получится бесконечно длинный соленоид. Поле внутри такого соленоида однородно т.к. повсюду все В одинаково направлены (вдоль оси соленоида) и равны по модулю.
