2.1 Алгоритм Дейкстры.
Переходим к описанию алгоритма Дейкстры. Рассмотрим сеть на рис.1
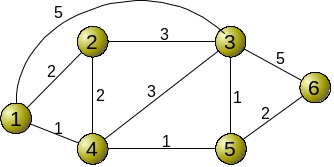
Рис.1 Пример сети
Числа, проставленные у каждой линии, указывают ее стоимость (ради простоты стоимость в обоих направлениях предполагается одинаковой; однако в более общем случае стоимость передачи в разных направлениях может и различаться). Алгоритм Дейкстры позволяет найти кратчайшие пути от источника ко всем другим узлам. Для этого требуется знание глобальной структуры, т.е. списка всех узлов сети и их взаимосвязей, а также стоимости каждой линии. Таким образом, алгоритм Дейкстры служит для централизованных вычислений с полной информацией о структуре, имеющейся на центральной базе данных. В примере на рис.1 целью является нахождение кратчайшего пути от узла 1, являющегося источником, ко всем остальным узлам сети. Алгоритм решает эту задачу поэтапно, строя дерево кратчайших путей с корнем в узле-источнике (в данном примере в узле 1), пока будет охвачен самый удаленный узел. На k-м шаге вычисляются кратчайшие пути к k-узлам, ближайшим к источнику. Они определяются как находящиеся внутри множества N. Опишем алгоритм неформально.
Обозначим через D(v) расстояние (сумму весов каналов вдоль данного пути) от источника 1 до узла v. Пусть l(i,j) - заданная стоимость пути между узлами i и j. Алгоритм состоит из двух частей: начального шага и итераций, повторяющихся до завершения алгоритма.
Начальный шаг. Устанавливаем N={1}. Для каждого узла v, не принадлежащего множеству N, устанавливаем D(v)=l(1,v). (Расстояние до узлов, не соединенных с узлом 1, принимаем равным ; практически можно принять любое число, большее максимальной стоимости или расстояния.)
Каждый последующий шаг. Находим не принадлежащий множеству N узел w, для которого D(w) минимально и включаем w в множество N. Затем обновляем значения D(v) для всех остальных узлов, не принадлежащих N путем вычисления
.
Шаг 2 повторяется, пока в множество N не войдут все узлы.
Применение алгоритма Дейкстры к сети на рис.1 иллюстрируется последовательными шагами, указанными в таблице1.1. Полужирным курсивом в столбцах обозначены минимальные значения D(w) на каждом шаге (при равных расстояниях выбор производится случайным образом). После каждого шага соответствующий узел w добавляется к N. Затем величины D(v) обновляются. Например, после начального шага во время шага 1 к множеству N добавляется узел 4, имеющий минимальное значение D(4)=1. На шаге 2 в N включается узел 5 при D(5)=2, и т.д. После шага 5 все узлы оказываются включенными в множество N, и алгоритм завершается.
Таблица1.1 Применение алгоритма Дейкстры к сети рис.1
-
Шаг
N
D(2)
D(3)
D(4)
D(5)
D(6)
Начальный
{1}
2
5
1
1
{1,4}
2
4
1
2
2
{1,4,5}
2
3
1
2
4
3
{1,2,4,5}
2
3
1
2
4
4
{1,2,3,4,5}
2
3
1
2
4
5
{1,2,3,4,5,6}
2
3
1
2
4
По мере работы алгоритма, приводящей к результатам, показанным в табл.1.1, в то же самое время строится дерево кратчайших путей с корнем в узле 1: при включении узла во множество N он соединяется с соответствующим узлом, уже принадлежащим N. Результирующее дерево для сети на рис.1 показано на рис.2а.
а
Получатель Следующий шаг
2 2
3 4
4 4
5 4
6 4
б
Рис.2. Применение алгоритма Дейкстры к рис.1;
источник-узел 1: (а) построение дерева кратчайших путей,
(б) таблицы маршрутов, узел 1.
Цифры в скобках у каждого узла указывают шаг, на котором этот узел был включен в дерево. С помощью дерева кратчайших путей для узла 1 можно получить таблицу маршрутов для узла 1, показывающую исходящий путь. По которому нужно направлять пакеты к узлу назначения. Подобная таблица маршрутов может быть составлена для каждого узла, являющегося источником сообщений. В случае централизованных вычислений каждая таблица маршрутов затем может быть направлена в соответствующий узел. В случае же децентрализованного, или распределенного выбора маршрутов, как в обсуждаемом ниже алгоритме сети ARPA, каждый узел выполняет свои вычисления, используя ту же самую глобальную информацию и генерируя собственное дерево и соответствующую таблицу маршрутов.