2.2. Операции над множествами

1) Объединение (сумма, дизъюнкция)

Х = А  В := {x | x  A v x  B}

«v» = «или» (см. рис. 2.2, а)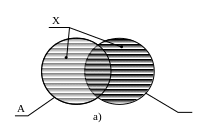

В

В

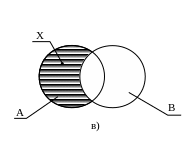
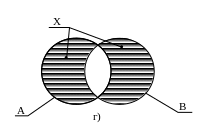
Рис. 2.2

2) Пересечение (произведение, конъюнкция)

Х = А  В := {x | x  A & x  B}

«&» = «и» (см. рис. 2.2, б).

3) Разность (см. рис. 2.2, в)

Х = А \ В := {x | x  A & x  B}.

4) Симметрическая разность (см. рис. 2.2, г)

Х = (А \ В)  (В \ А) = А Δ В := {x | x  A & x  B, x  В & x  А }.

5) Дополнение

.

Элементы всех множеств можно считать элементами некоторого универсального множества U – универсума, который играет роль единицы. Тогда разность U \ A называется дополнением множества А и часто обозначается (-А) или (¬А).

2.3. Свойства операций над множествами

1) Идемпотентность: А  А = А, А  А = А.

2) Коммутативность: А  В = В  А,А  В = В  А.

3) Ассоциативность: А  (В  С) = (А  В)  С,

А  (В  С) = (А  В)  С.

4) Дистрибутивность: А  (В  С) = (А  В)  (А  С),

А  (В  С) = (А  В)  (А  С).

5) Поглощение: (А  В)  А = А, (А  В)  А = А.

6) Свойства нуля: А   = , А   = А.

7) Свойства единицы: А  U = A, А  U = U.

8) Инволютивность: .

9) Законы де Моргана: , .

10) .

11) .

12) Рефлексивность: А  А.

13) Транзитивность: если А  В и В  С, то А  С.

Алгебраическая операция определена на А, если можно указать закон, по которому любой паре (a, b) из АА ставится в соответствие третий элемент, принадлежащий этому же множеству.

c = a + b – сложение, с = ab – умножение, c = ab – в общем случае.

Основные свойства операций: коммутативность и ассоциативность.

Операция – это всегда отношение, но не наоборот.

Множество К называется кольцом, если в нем определены операции сложения и умножения, обе ассоциативны и дистрибутивны, причем сложение коммутативно и обладает обратной операцией.

Множество К называется линейным или векторным пространством, если для элементов (векторов) из К определены операции сложения и умножения на число Р и выполняются аксиомы:

1) Каждой паре векторов (х, у) отвечает вектор (х + у) и называется суммой, причем х + у = у + х (коммутативность) и х + (у + z) = (х + у) + z (ассоциативность).

Существует единственный нулевой вектор О такой, что х + О = х, х.

Существует вектор (-х) такой, что х + (-х) = О.

2) Каждой паре (, х), где  - число, а х – вектор, отвечает вектор х, причем:

 ( х) = ( ) х, 1х = х.

3) (х + у) = х + у, ( + )х = х + х.

2.4. Алгебры

Множества и функции на них – это два типа объектов, на которых в конечном счете строится любая математическая теория.

Если аргументы функции f пробегают множество М и она принимает значения из того же множества, то f – это алгебраическая операция на М.

Итак, алгебра – это множество М вместе с набором операций на нем. Обозначается алгебра как двойка (М, ), где :={₁, ₂, …, _n} – набор (множество) операций, сигнатура алгебры, а М – носитель алгебры.

Группой называется множество, если:

1) выполняется условие наличия одной ассоциативной операции;

2) в группе есть элемент «е», удовлетворяющий условию a^.e = e^.a = a, он называется «единицей»;

3) для каждого элемента а существует единственный элемент (а^-1) такой, что

a^.a^-1 = e, (a^-1)^.a = e.

Если, кроме того, для a, b G имеет место коммутативность a^.b = b^.a, то группа называется коммутативной или абелевой.