Көп қызметті статистикалық критерийлер

Көп қызметті критерийлер дегеніміз әртүрлі берілгендерге, таңдауларға және есептерге қатысты қолданылатын критерийлерді айтамыз. Бұл дегеніміз мәліметтер кез келген шкалада ұсынылуы мүмкін.

Сонымен қатар, таңдаулар тәуелсіз, тәуелді, яғни біз көп қызметті критерийлер көмегімен зерттелінушілердің түрлі таңдауларын және түрлі шарттардағы бір таңдаулар көрсеткіштерін салыстыра аламыз. Төменгі таңдау шегі -5 бақылау, тек биномиальды критерийде жоғарғы шегі 50 адам, Фишердің φ* критерийінде жоғарғы шек болмайды, таңдаулар саны өте көп те болуы мүмкін. Көп қызметті критерийге Фишердің φ* критерийі және биномиальды m критерийді жатқызуға болады.

Көп қызметті критерий бірлік немесе пайыздық үлесте құрылады. Критерийдің мағынасы болып берілген таңдауда зерттеушіге қандай әсер қызықтырады және әсердің қандай бөлшегі сипатталмайтыны болып табылады.

Мұндай әсерлер:

1. Белгіні нақты анықтайтын нақты мән –мысалы, қандай да бір ұсыныспен келісу, екі симметриялы жолдың оң жолын таңдау, нақты жынысқа жатқызу.

2. Белгінің санын өлшейтін нақты деңгей, мысалы, есепті 20 сек.ішінде шығару, проходной баллдан асатын бағаны алу.

Зерттелініп жатқан белгі деңгейінде немесе мәнінде қатынасты анықтау, мысалы, А және Б альтернативті таңдауларын В және Г таңдаларына қарағанда жиі таңдау, оң жылжулардың сол жылжуларға қарағанда көп болуы және т.б.

Осылайша кез келген мәліметтердің «әсер бар –әсер жоқ» баламалық шкаласындағы көп қызметті критерий деңгейлерді салыстыру, жылжуларды бағалау, орнатуларды салыстыру үш есебін шешуге мүмкіндік береді.

φ* критерийі екі таңдау болған жағдайда, биномиальды m критерийі тек бір таңдау болған жағдайда қолданылады.

Крускал-Уоллистің Н критерийі

Критерийдің қойылуы

Бұл критерий қандай да бір белгінің деңгейінде, бір уақытта үш, төрт және т.б. таңдаулар арасында айырмашылықты бағалау үшін арналған. Ол белгі деңгейінің бір топтан екінші топқа өзгеруін көрсетеді, бірақ бұл өзгерістің бағытын көрсете алмайды.

Критерийді сипаттау. Н критерийі дисперсионды бір факторлы талдаудың параметрлік емес аналогы ретінде қарастырылады. Кейде бұл критерийді рангілер қосындысы деп те атайды. Мұнда барлық жеке мәндердің қосындысы алынып, үлкен бір таңдау ретінде қарастырылады. Барлық жеке мәндер бастапқы таңдауға қайтарылып, әрбір таңдаудағы ранг қосындыларын есептейміз. Егер таңдау арасындағы айырмашылық кезедейсоқ болса, ранг қосындылары арасында қатты айырмашылық болмайды, себебі жоғарғы және төменгі рангілер таңдаулар арасында бірқалыпты бөлінеді. Егер бір таңдауда төмен ранг, ал басқасында өте жоғары, үшіншісінде орташа болса, Н критерийі осы айырмашылықты орнатады.Болжамдар.

Н₀: 1,2,3 және т.б. таңдаулар арасында зерттеліп отырған деңгей бойынша тек кездейсоқ айырмашылықтар болады.

Н₁:1,2,3 және т.б. таңдаулар арасында зерттеліп отырған деңгей бойынша кездейсоқ емес айырмашылықтар болады.

Н критерийінің шектері

1. Үш таңдауды сәйкестендіргенде тек біреуінде ғана п=3, ал қалған екеуінде n=2 болуы мүмкіндігін жібереді. Бірақ мұндай сандық құрамда таңдауды (р≤0,05)төменгі деңгейінде орната аламыз.

2. Н критерийінің шекті мәндері және оған сәйкес деңгейлері келесі Қосымша 1-ң 1-кестесінде келтірілген. Кестеде тек үш таңдау және {n₁, n₂, n₃}≤5 қарастырылған. Таңдау және бақылаулар санының көп болуына байланысты χ² критерийінің шекті мәндерінің кестесін қолдану қажет, себебі Крускал-Уоллис критерийі χ² орнатуына асимптотикалық жақын орналасқан.

Есептеу алгоритмі:

Крускал-Уоллистің Н критерийін есептеу алгоритмі

1. зерттеушілердің барлық көрсеткішін жеке карточкаларға көшіру

2. 1-топ зерттеушілерінің карточкаларын бір түспен, мысалы, қызыл, сол сияқты қалған зерттеушілердің де парақтарын сәйкесінше белгілеу керек.

3. барлық карточкаларды бір қатарға белгінің өсу ретіне байланысты (карточканың қай топ екенін қарамаймыз) орналастырамыз.

4. карточкалардағы мәндерді (ранжирлерлеймиз) қоямыз, яғни ең кіші мәнге төменгі мәнді сәйкестендіреміз.әрбір карточкаға өзінің рангысын жазып қоямыз. Рангының жалпы саны таңдаудың жалпы тәжірибенің санына тең.

5. карточкаларды топ бойынша түсіне немесе басқа белгілерге қарап қайтадан бөлеміз

6. әрбір топ бойынша рангылердің қосындысын табамыз. Жалпы ранг қосындысы мен есептеу рангысының сәйкестігін тексереміз.

7. Н критерийін келесі формула бойынша есептейміз:

Мұндағы N – біріктірілген таңдаудағы зерттеудің жалпы саны;

n – әрбір топтағы зерттеу саны;

Т – әрбір топ бойынша ранг қосындысы суммы.

8а. с=3 топ саны кезінде , n₁•n₂•n₃≤5шекті мәндер мен оларға сәйкес мәндер деңгейін анықтау (кесте-4, қосымша 1).

ЕгерН_эмп равен или превышает критическое значение H_0,05 шекті мәндерге тең немесе асса, онда H₀есептелмейді.

8б. егер топ саны с>3 немесе зерттеу саны n₁•n₂•n₃>5 болса,онда χ² шекті мәндерді Қосымша 1 9-кесте бойынша анықтау керек.

Егер Н_эмпχ² мәніне тең немесе үлкен болса, онда H₀есептелмейді.

Н критерийінің шектеулері

1. Үш таңдауды сәйкестендіргенде тек біреуінде ғана п=3, ал қалған екеуінде n=2 болуы мүмкіндігін жібереді. Бірақ мұндай сандық құрамда таңдауды (р≤0,05)төменгі деңгейінде орната аламыз.

2. Н критерийінің шекті мәндері және оған сәйкес деңгейлері келесі Қосымша 1-ң 1-кестесінде келтірілген. Кестеде тек үш таңдау және {n₁, n₂, n₃}≤5 қарастырылған. Таңдау және бақылаулар санының көп болуына байланысты χ² критерийінің шекті мәндерінің кестесін қолдану қажет, себебі Крускал-Уоллис критерийі χ² орнатуына асимптотикалық жақын орналасқан.

Пейдж өзгерісінің L – критерийі

Өзгерістің L – критерийін тағайындау

Пейдждің L критерийі бір зерттелінушілерге жүргізілетін үш немесе одан көп шарттардың көрсеткіштерін салыстыруда қолданылады. Критерий бір шарттан екінші шартқа ауысқандағы белгі шамасының өзгеру бағытын анықтайды. L өзгеру критерийін сипаттау

Критерий белгіленген жасқа немесе жағдайларға байланысты белгілердің динамикасын тексеруге мүмкіндік береді. Ол бір өлшемнен екінші өлшемге ауысқанда мәндердің өзгеру бағыты туралы бір болжамға бірнеше өлшемдерді біріктіруге мүмкіндік береді. Бірақ крикалық мәннің кестесі тек (n<12) таңдауларға және (с<6) өлшемдер санына есептелген. Егер бұл шектеулер орындалмаса, онда Фридманның χ²_r критерийін қолдануға тура келеді.L критрийі χ²_r критерийі сияқты әрбір зерттелінушілердің шарттарын орнатады. Егер зерттелінуші бірінші тәжірибеде 17 қате, екіншіде 12, үшіншіде 5 қате жіберсе, онда үшінші шартқа 1-ші ранг, екінші шарт 2-ранг, ал бірінші шарт 3-рангті алады. Барлық мәнге рангтерін орналастырғаннан кейін, әрбір баған бойынша ранг қосындылары есептеледі. Содан кейін бағандар ранг қосыныдыларының өсу ретімен орналасады: бірінші орында ең аз ранг қосыныдысы бағаны, т.с.с. ең соңында ранг қосыныдысының ең үлкен бағаны орналасады. Ары қарай L есептеуінің аранайы формуласы бойынша мәннің солдан оңға қарай шынымен де өсетінін тексереміз. L критерийінің эмпирикалық мәні ранг қосыныдыларының арасындағы айырмашылықты көрсетеді. Сондықтан L мәні көп болған сайын айырмасы нақтырақ болады.Болжамдар

Н₀: Бірінші шарттан екінші шартқа, одан кейін үшіншіге және т.с.с ауысқандағы жеке көрсеткіштердің өсуі кездейсоқ.

H₁: Бірінші шарттан екінші шартқа, одан кейін үшіншіге және т.с.с ауысқандағы жеке көрсеткіштердің өсуі кездейсоқ емес.

Болжамды құрастырғанда өзгеріске сәйкес келетін шарттардың жаңа номерлеулерін есепке аламыз.

Пейдж критерийінің шектеулері

1. Төменгі шектеу – әртүрлі шартта 3 өлшемнен кем емес кемінде 2 адам. Жоғарғы шегі - 12 адам және 6 шарт (n≤12, c≤6). L критерийінің критикалық мәндері J.Greene, M. D'Olivera (1989) басшылығымен берілген. Олар статистикалық мәннің үш деңгейін қарастырады: р≤0,05; р≤0,01; р≤0,001.

2. Тестті қолданудың негізгі шарты мәліметтердің реттелгендігі: көрстекіштің ең аз рангілік қосындысыс сол жақта, оң жақта ең үлкені. // Барлық бағандарды номерлеп, одан кейін солдан оңға қарай есепті жүргіссек болады, бірақ бұл жағдайда шатасу оңай.

Пейдж өзгеруінің L критерийі

1.Бірінші зерттелінушінің 1-ші, 2-ші, 3-ші т.с.с. өлшемдерде алынған жеке мәндерді орындарына қою.

Сонымен қатар бірінші зерттелінуші ретінде алфавит бойынша басталуы да мүмкін.

2.Осыны барлық зерттелінушілерге орындап шығу керек.

3.Шарттар бойынша ранг қосындыларын аламыз. Жалпы ранг қосындысы мен есептеу ранг қосындысының теңдігін тексереміз.

4.Кестедегі ранг қосындыларын өсу ретімен орналастырамыз.

5.L эмпирикалық мәнін келесі формула бойынша анықтаймыз:

мұндағыT_i – берілген шарт бойынша ранг қосындысы;

j - жаңа тізбекте әрбір шартқа тіркелген реттелген номер.

6. Қосымша 1-дің VIII кестесі бойынша Lкритикалық мәнді. Егер L_эмпмән критикалық мәнге тең немесе одан үлкен болса, өзгеру анық болып есептеледі.

Рангтік бірфакторлы талдау.

РАНГОВЫЙ ОДНОФАКТОРНЫЙ АНАЛИЗ Если ничего не известно о распределении неизвестных, то использовать для проверки гипотезы количественные наблюдения становится затруднительно. В этих случаях проще основывать свои выводы на отношениях "больше – меньше" между наблюдениями, т.к. они не зависят от вида распределения. Теперь вся информация, включенная в табл. 1, содержится в тех рангах, что, получают числа при упорядочении всей совокупности (направление упорядочивания min→max, или max→min – не существенно). Тогда таблица 1 преобразуется в таблицу 2:

Таңдауларды деңгей және белгілерді орнату бойынша салыстыру

Критерийді қолдану берілген нұсқау бойынша белгілерді қандай да бір деңгейде салыстырып, кейіннен белгілердің екі таңдауда орналасуын тексереміз. Мұндай есеп диапазонда айырмашылықты талдауда немесе қандай да бір жаңа әдіс бойынша зерттелінушілерден алынған бағалауды орнату формасында шешу маңызды.Р. Т. Чиркин(1995) зерттеуінде алғаш рет жадыдан аттарды, фактілерді шығарып тастау және отбасылық, жеке, кәсіби комплекстерге негізделген іс әрекеттер әдістеріне сауалдама құрылды. Таңдау отбасы құрмаған 17 мен 20 жас аралығындағы педагогикалық институттың 50 студенттеріне жүргізілді. Осы сауалдама көмегімен олар өздерінің кемшілігін немесе «комплекстерін» анықтай алады. Нәтиже төмендегі кестеде көрсетілген.Сауалдама көмегімен сыртқа шеттеу және өзінің кемшілік белсенділігі көрсеткіштері арасында айырмашылықтың бар екеніне тұжырым жасай аламыз ба? Өзінің кемшілігін сезіну белсенділігі көрсеткішінің топтардағы студенттердің жоғары (n1=18) және төмен(n2=24) шеттеу энергиясы

Топ 1: шеттету энергиясы 19-дан 31 баллға дейін (n1=18)		Топ 2: шеттету энергиясы 7-ден 13 баллға дейін (n2=24)
0; 0; 0; 0; 0 20; 20 30; 30; 30; 30; 30; 30; 30 50; 50 60; 60		0; 0 5; 5; 5; 5 10; 10; 10; 10; 10; 10 15; 15 20; 20; 20; 20 30; 30; 30; 30; 30; 30
қосындысы орташа	470 26,11	370 15,42

Топтағы шеттету энергиясының орташа шамасы жоғары болғанына қарамастан, ол жақта 5 нольдік мән бар. Егер екі таңдаудағы бағалауды орнатудың гистограммасын салыстырсақ, айырмшылық контрастын байқаймыз:

φ* критерийі графиктегі екі орнатудың сәйкес емес әсерлерін тексеруге мүмкіндік береді. Егер «әсер барды» кемшілікті сезіну көрсеткіші өте төмен 0 немесе өте жоғары 30 болғанда, және керісінше, «әсер жоқты» орташа мәні 5-тен 25-ке дейінгі мәндерді қабылдайды деп есептейік.

Болжамдар:

H₀: Кемшілігін сезіндегі (не 0, не 30 және одан да жоғары болған жағдайда) шеттету көрсеткішінің топтағы энергиясы көп жақ топтың энергиясы төмен жақ энергиясына қарағанда жиі кездеспейді.

H₁:Кемшілігін сезіндегі (не 0, не 30 және одан да жоғары болған жағдайда) шеттету көрсеткішінің топтағы энергиясы көп жақ топтың энергиясы төмен жақ энергиясына қарағанда жиі кездеседі.

φ*критерийін есептеу үшін кесте құрайық.

Топтар	"Әсер бар": кемшілігі бар көрсеткіш 0 тең немесе >30		"Әсер жоқ": кемшілігі бар көрсеткіш 5-тен 25 дейін		қосынды
1 топ – энергиясыжоғары шеттету мен	16	(88,9%)	2	(11,1%)	18
2 топ - с энергиясы төмен шеттетумен	8	(33,3%)	16	(66,7%)	24
қосынды	24		18		422

Қосымша 1-ң XIII кестесінен «әсер» пайыздық үлесінің әр топтағы φ шамасын сәйкесінше анықтаймыз:

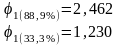
φ*эмпирикалық мәнін есептейміз:

φ* критикалық мәні кез келгенn₁, n₂төмендегі мәндерге тең:

Қосымша 1-ң XIII кестесіалынған нәтиженің р<0,001 мәндегі деңгейін нақты анықтауға мүмкіндік береді.

Жауабы: H₀ескерілмейді. H₁ қабылданады.Кемшілігін сезіндегі (не 0, не 30 және одан да жоғары болған жағдайда) шеттету көрсеткішінің топтағы энергиясы көп жақ топтың энергиясы төмен жақ энергиясына қарағанда жиі кездеседі.