4.2.5 Расчет переходных процессов ударного приложения нагрузки
Расчет переходных процессов при ударном приложении и снятии нагрузки
При ударном приложении снятии нагрузки АД работает на линейном участке механической характеристики ( ).
С учетом электромагнитной инерции силовой цепи АД (TЭ) переходные процессы описываются уравнением механической характеристики АД и уравнением движения механической части
|
(1) |
где
–
электромагнитная постоянная времени
силовой цепи;
– электрическая
скорость поля статора при частоте f1Н.
Решив второе уравнение системы (1) относительно M и подставив в первое, получим дифференциальное уравнение относительно скорости ω
|
(2) |
,где
– перепад скорости под действием момента
нагрузки
.
Аналогично получим дифференциальное уравнение для момента
|
(3) |
.Характеристическое уравнение
|
(4) |
.
При
корни
характеристического уравнения комплексные
где
;
.
При комплексных корнях характеристического уравнения решение уравнения (2) запишется в виде
|
(5) |
.Выражение для коэффициентов A и B получим из начальных условий.
При t = 0;
,
;
;
.
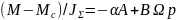Тогда
;
.
Решение уравнения изменения скорости во времени примет вид
|
(6) |
.При m < 4 общее решение (2) для момента будем искать в виде
|
(7) |
.Из начальных условий
При t = 0; ; согласно с первым уравнением системы (1)
получим
величина
где
.
Тогда при подстановке и в (7) получим
,
,
Решение уравнения (7) примет вид
|
(8) |
.При m > 4 корни характеристического уравнения действительные отрицательные
и
В этом случае общее решение уравнения для скорости запишется в виде
|
(9) |
.При t = 0,
, |
(10) |
. |
(11) |
Определив из (10) коэффициент B1
|
(12) |
и
подставив B1
в (11) получим выражение для коэффициента
|
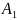
(13) |
.Подставив (13) в (12) получим выражение для коэффициента В1
|
(14) |
.Подставив
и
в (9) получим
|
(15) |
.Общее решение уравнения для момента двигателя
|
(16) |
При t = 0 ,
,
где .
Совместное решение уравнений
|
(17) |
дает значение коэффициентов
После
подстановки
и
в (16) выражение для M
принимает вид
|
(18) |
В
случае, когда m
= 4
корни характеристического уравнения
решение для скорости имеет вид
|
(19) |
.При
t
= 0,
,
,
,
.
подставив
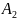и
в (19) получим
|
(20) |
.Общее решение уравнения для момента
|
(21) |
,при
t
= 0,
,
;
;
.
Подставив
и
в (21) получим
|
(22) |
.
Полученные
соотношения для скорости ω
и момента M
позволяют рассчитать переходные процессы
пуска, реверса, торможения, перехода с
одной скорости на другую при приложении
и снятии нагрузки, для случая
и сочетаниях параметров m
< 4,
m
= 4
и m
> 4
при подстановке в них начальных условий.
Для
конкретного случая ударного приложения
нагрузки (в момент времени t
= 0
нагрузка скачком увеличивается от
до
).
АД
работает на естественной характеристике
при S
< SK,
т.е. характеристика АД линейна. Рассмотрим
случай, когда m
< 4,
что соответствует комплексным корням
характеристического уравнения. Так как
предшествующий режим был установившимся
(рис. 4, а), в (6) и (8)
и
.
Учитывая, что
;
,
уравнение (6) примет вид
|
(23) |
.При
записи (8) и учете, что
получаем
|
(24) |
|
|
||
а) |
б) |
|
Рис. 4. Переходный процесс ударного приложения нагрузки |
||
.
На
рис. 4, б приведены зависимости
и
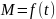при m
= 1.
Сравним естественную механическую
характеристику 1
(рис.4,а), с построенной с помощью графиков
переходных процессов (рис.4,б), динамической
механической характеристикой 2
(рис. 4, а).
При
приложении скачком момента нагрузки
идет процесс снижения скорости,
приводящий, в свою очередь, к росту
момента двигателя. Однако, вследствие
наличия индуктивности силовой цепи
нарастание момента двигателя идет
медленнее, а скорость снижается в большей
степени, чем это определяется статической
характеристикой 1.
При достижении моментом двигателя М
значения момента сопротивления
скорость
,
что ведет к дальнейшему росту момента
до
.
Колебания затухают, и достигается
установившийся режим
и
.
Максимальное
динамическое падение скорости
при этом превышает статическое падение
тем в большей степени, чем больше
жесткость статической характеристики
и чем больше
.
Отклонение скорости от требуемого
значения из-за электромагнитной инерции
существенно увеличивается, что для ряда
механизмов, работающих с ударной
нагрузкой по условиям технологического
процесса, является неблагоприятным.
Расчет графиков переходных процессов, на основании полученных аналитических соотношений для M и ω можно провести на основании исходных дифференциальных уравнений на ЭВМ, используя метод Эйлера [2].
В качестве примера рассмотрим расчет переходных процессов на ЭВМ при ударном приложении нагрузки от 0,1MС до MН в электроприводе с асинхронным двигателем МТF411–6 (см. таблицу П.1).
Параметр |
Ед. изм. |
Двигатель |
|||
Тип |
- |
МTF411–6 |
|||
Pном |
кВт |
27 |
|||
nном |
об/мин |
955 |
|||
Mк/Мном |
- |
3,0 |
|||
cosφ |
ном. |
- |
0,77 |
||
хол.х |
- |
0,077 |
|||
Статор |
Ic.ном |
А |
64 |
||
Ic.х |
А |
40 |
|||
Rc |
Ом |
0,197 |
|||
Xc |
Ом |
0,287 |
|||
Ротор |
Ep.ном |
В |
246 |
||
Iр.ном |
А |
77 |
|||
Rp |
Ом |
0,077 |
|||
Xp |
Ом |
0,236 |
|||
Коэффициент трансформации напряжения
|
- |
2,37 |
|||
Момент инерции ротора Jp |
кг·м2 |
2,0 |
|||
Расчет параметров двигателя ведётся в следующем порядке:
Определяется скорость идеального холостого хода
Определяется номинальный момент двигателя
Определяется критический момент двигателя
Определяются активные и индуктивные сопротивления статора и ротора
Определяется номинальное скольжение двигателя
Определяется жесткость механической характеристики двигателя
Определяются механическая и электромагнитная постоянные времени двигателя
Так как m < 4, то корни характеристического уравнения комплексно-сопряженные, а переходные процессы будут колебательными.
Программа для расчета переходных процессов методом Эйлера в пакете MathCad представлена ниже. В программе приняты следующие обозначения: ω0 = w0, ω = w, Tэ = Tе, β = b.
Скорость идеального холостого хода
w0 := 104.7
Электромагнитная постоянная времени
Te := 0.013
Момент инерции
J := 2
Жесткость механической характеристики
b := 62
Момент сопротивления
Шаг интегрирования
h := 0.001
Количество шагов
n := 0 .. 750
Начальные значение времени, момента и скорости:
t0 := 0 M0 := 0 w0 := 0
Решение системы уравнений методом Эйлера
Результаты расчета переходных процессов
Приложение 1
Краново-металлургические двигатели с фазным ротором типа МТ, U1=380 В
Таблица П.1.
Параметр |
Ед. изм. |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
Тип |
- |
МТ21–6 |
МТ22–6 |
МТ31–6 |
МТ31–8 |
МТ41–8 |
МТ42–8 |
МТ51–8 |
МТ52–8 |
МТ61–14 |
МТ62–10 |
|
Pном |
кВт |
5 |
7,5 |
11 |
7,5 |
11 |
16 |
22 |
30 |
30 |
45 |
|
nном |
об/мин |
940 |
945 |
953 |
702 |
715 |
718 |
723 |
725 |
574 |
577 |
|
Mк/Мном |
- |
2,9 |
2,8 |
3,1 |
2,6 |
2,9 |
3,0 |
3,0 |
3,0 |
3,3 |
3,2 |
|
cosφ |
ном. |
- |
0,68 |
0,69 |
0,71 |
0,69 |
0,67 |
0,69 |
0,7 |
0,74 |
0,67 |
0,71 |
хол.х |
- |
0,52 |
0,27 |
0,24 |
0,22 |
0,22 |
0,22 |
0,23 |
0,23 |
0,2 |
0,18 |
|
Статор |
Ic.ном |
А |
14,9 |
20,9 |
28,4 |
21,2 |
30,8 |
42,5 |
56,5 |
71,6 |
80 |
110 |
Ic.х |
А |
10,9 |
15,0 |
19,2 |
16,7 |
22,2 |
29,6 |
36,1 |
44,0 |
55,0 |
71,0 |
|
Rc |
Ом |
1,11 |
0,685 |
0,415 |
0,788 |
0,43 |
0,271 |
0,179 |
0,136 |
0,1125 |
0,0625 |
|
Xc |
Ом |
1,07 |
0,735 |
0,465 |
0,898 |
0,515 |
0,354 |
0,297 |
0,225 |
0,273 |
0,186 |
|
Ротор |
Ep.ном |
В |
164 |
227 |
200 |
185 |
155 |
222 |
197 |
257 |
142 |
206 |
Iр.ном |
А |
20,6 |
21,6 |
35,4 |
28,0 |
46,7 |
46,3 |
70,5 |
74,3 |
133 |
138 |
|
Rp |
Ом |
0,24 |
0,29 |
0,132 |
0,211 |
0,0835 |
0,105 |
0,0496 |
0,136 |
0,0225 |
0,028 |
|
Xp |
Ом |
0,72 |
0,544 |
0,27 |
0,38 |
0,171 |
0,239 |
0,0593 |
0,174 |
0,0382 |
0,0574 |
|
Коэффициент трансформации напряжения
|
- |
2,2 |
1,6 |
1,84 |
1,94 |
2,33 |
1,63 |
1,84 |
1,41 |
2,47 |
4,37 |
|
Момент инерции ротора Jp |
кг·м2 |
0,1 |
0,142 |
0,262 |
0,262 |
0,465 |
0,675 |
1,1 |
1,42 |
3,25 |
4,37 |
|
Краново-металлургические двигатели с фазным ротором типа МIТ, U1=380 В
Таблица П.2.
Параметр |
Ед. изм. |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
Тип |
- |
М1Т111–6 |
М1Т112–6 |
М1Т211–6 |
М1Т311–6 |
М1Т312–6 |
М1Т411–6 |
М1Т412–6 |
М1Т511–8 |
М1Т512–8 |
М1Т611–10 |
|
Pном |
кВт |
3,5 |
5,3 |
8,2 |
13 |
17,5 |
27 |
36 |
34 |
45 |
50 |
|
nном |
об/мин |
870 |
885 |
900 |
925 |
945 |
950 |
955 |
695 |
695 |
560 |
|
Mк/Мном |
- |
1,2 |
2,0 |
2,0 |
2,5 |
2,4 |
3,0 |
3,1 |
2,3 |
3,0 |
3,2 |
|
cosφ |
ном. |
- |
0,72 |
0,76 |
0,7 |
0,74 |
0,77 |
0,77 |
0,75 |
0,77 |
0,79 |
0,76 |
хол.х |
- |
0,154 |
0,123 |
0,112 |
0,095 |
0,0916 |
0,08 |
0,071 |
0,07 |
0,08 |
0,08 |
|
Статор |
Ic.ном |
А |
11,6 |
15,3 |
24,6 |
35 |
43 |
65 |
87 |
82 |
104 |
128 |
Ic.х |
А |
9,87 |
11,8 |
19 |
23,2 |
34,4 |
39,7 |
51,8 |
47,4 |
53,1 |
78,1 |
|
Rc |
Ом |
2,62 |
1,61 |
0,835 |
0,51 |
0,337 |
0,219 |
0,139 |
0,164 |
0,103 |
0,085 |
|
Xc |
Ом |
1,7 |
1,14 |
0,88 |
0,645 |
0,431 |
0,271 |
0,197 |
0,232 |
0,172 |
0,18 |
|
Ротор |
Ep.ном |
В |
178 |
217 |
257 |
186 |
233 |
247 |
271 |
297 |
319 |
197 |
Iр.ном |
А |
16,5 |
19 |
23 |
51 |
54 |
77 |
88 |
81 |
94 |
185 |
|
Rp |
Ом |
0,671 |
0,603 |
0,466 |
0,124 |
0,125 |
0,08 |
0,059 |
0,124 |
0,091 |
0,0278 |
|
Xp |
Ом |
0,565 |
0,625 |
0,666 |
0,241 |
0,254 |
0,233 |
0,173 |
0,448 |
0,356 |
0,176 |
|
Коэффициент трансформации напряжения
|
- |
4,54 |
3,1 |
2,18 |
4,2 |
2,66 |
2,37 |
1,96 |
1,645 |
1,415 |
3,72 |
|
Момент инерции ротора Jp |
кг·м2 |
0,195 |
0,27 |
0,46 |
0,9 |
1,25 |
2,0 |
2,7 |
4,3 |
5,7 |
17 |
|
Обмотка статора соединена в звезду, линейное напряжение обмотки статора Uл = 380 В, fн = 50 Гц.
Краново-металлургические двигатели с фазным ротором типа МTF, U1=380 В
Таблица П.3.
Параметр |
Ед. изм. |
U |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
Тип |
- |
МTF012–6 |
МTF111–6 |
МTF112–6 |
МTF211–6 |
МTF311–6 |
МTF312–6 |
МTF311–8 |
МTF312–8 |
МTF411–6 |
МTF411–8 |
|
Pном |
кВт |
2,7 |
4,1 |
5,8 |
9 |
13 |
17,5 |
9 |
13 |
27 |
18 |
|
nном |
об/мин |
840 |
874 |
915 |
915 |
935 |
950 |
680 |
695 |
955 |
700 |
|
Mк/Мном |
- |
1,9 |
1,9 |
2,4 |
2,1 |
2,5 |
2,4 |
2,0 |
2,5 |
3,0 |
2,5 |
|
cosφ |
ном. |
- |
0,74 |
0,79 |
0,74 |
0,74 |
0,74 |
0,77 |
0,74 |
0,76 |
0,77 |
0,73 |
хол.х |
- |
0,14 |
0,108 |
0,105 |
0,085 |
0,095 |
0,085 |
0,108 |
0,08 |
0,077 |
0,083 |
|
Статор |
Ic.ном |
А |
8,9 |
11,7 |
16 |
24 |
34,5 |
42,5 |
25,6 |
34 |
64 |
46,7 |
Ic.х |
А |
6,12 |
7,45 |
11,35 |
14,35 |
23,2 |
28,7 |
17,7 |
24,2 |
40 |
29,8 |
|
Rc |
Ом |
3,63 |
2,1 |
1,26 |
0,755 |
0,48 |
0,23 |
0,835 |
0,365 |
0,197 |
0,327 |
|
Xc |
Ом |
2,51 |
1,93 |
1,26 |
1,05 |
0,645 |
0,334 |
0,834 |
0,53 |
0,287 |
0,53 |
|
Ротор |
Ep.ном |
В |
154 |
175 |
217 |
273 |
184 |
233 |
264 |
178 |
246 |
221 |
Iр.ном |
А |
15 |
18,7 |
19,0 |
25 |
51 |
54 |
26 |
53 |
77 |
59 |
|
Rp |
Ом |
0,745 |
0,6 |
0,5 |
0,485 |
0,111 |
0,107 |
0,46 |
0,112 |
0,077 |
0,117 |
|
Xp |
Ом |
0,59 |
0,57 |
0,648 |
0,855 |
0,241 |
0,244 |
0,643 |
0,182 |
0,236 |
0,26 |
|
Коэффициент трансформации напряжения
|
- |
6,06 |
4,65 |
3,1 |
1,92 |
4,2 |
2,66 |
2,07 |
4,54 |
2,37 |
2,44 |
|
Момент инерции ротора Jp |
кг·м2 |
0,115 |
0,197 |
0,27 |
0,46 |
0,9 |
1,25 |
1,1 |
1,55 |
2,0 |
2,15 |
|
Краново-металлургические двигатели с фазным ротором типа МTМ, U1=380 В
Таблица П.4.
Параметр |
Ед. изм. |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
Тип |
- |
МTМ211–6 |
МTМ311–6 |
МTМ311–8 |
МTМ312–6 |
МTМ312–8 |
МTF411–6 |
МTМ411–8 |
МTМ412–6 |
МTМ511–8 |
МTМ512–8 |
|
Pном |
кВт |
5,0 |
7,0 |
5,0 |
11,0 |
7,5 |
16 |
11 |
22 |
22 |
30 |
|
nном |
об/мин |
920 |
945 |
685 |
950 |
695 |
975 |
740 |
960 |
715 |
716 |
|
Mк/Мном |
- |
2,5 |
2,5 |
2,5 |
2,8 |
2,5 |
2,8 |
2,8 |
2,8 |
2,8 |
2,8 |
|
cosφ |
ном. |
- |
0,75 |
0,73 |
0,73 |
0,76 |
0,74 |
0,78 |
0,7 |
0,8 |
0,73 |
0,73 |
хол.х |
- |
0,1 |
0,095 |
0,12 |
0,09 |
0,105 |
0,075 |
0,085 |
0,07 |
0,07 |
0,07 |
|
Статор |
Ic.ном |
А |
13,6 |
20 |
14,7 |
27,3 |
20,6 |
38,0 |
30,0 |
48,5 |
55 |
72 |
Ic.х |
А |
9,7 |
14,2 |
10,2 |
17,8 |
13,9 |
21,4 |
21 |
24,2 |
37 |
46 |
|
Rc |
Ом |
1,41 |
0,9 |
1,76 |
0,595 |
1,04 |
0,323 |
0,465 |
0,218 |
0,205 |
0,141 |
|
Xc |
Ом |
1,29 |
0,663 |
1,24 |
0,485 |
0,833 |
0,308 |
0,543 |
0,312 |
0,284 |
0,214 |
|
Ротор |
Ep.ном |
В |
215 |
240 |
215 |
166 |
254 |
200 |
172 |
225 |
237 |
288 |
Iр.ном |
А |
16,2 |
19,7 |
17,0 |
43,0 |
20 |
53,0 |
41,5 |
63,0 |
58,8 |
65,0 |
|
Rp |
Ом |
0,58 |
0,35 |
0,517 |
0,097 |
0,0462 |
0,092 |
0,116 |
0,072 |
0,106 |
0,102 |
|
Xp |
Ом |
0,66 |
0,511 |
0,664 |
0,181 |
0,641 |
0,235 |
0,214 |
0,225 |
0,231 |
0,252 |
|
Коэффициент трансформации напряжения
|
- |
1,76 |
1,51 |
1,67 |
2,2 |
1,41 |
1,8 |
2,1 |
1,63 |
1,53 |
1,26 |
|
Момент инерции ротора Jp |
кг·м2 |
0,115 |
0,225 |
0,275 |
0,312 |
0,387 |
0,5 |
0,537 |
0,675 |
1,025 |
1,4 |
|
Библиографический список
1. Онищенко Г.Б. Электрический привод: учебник для студентов высших учебных заведений/ Г.Б. Онищенко – М. Издательский центр «Академия», 2006. – 288с.
2. Ключев В.И. Теория электропривода: учебник для студентов вузов.3-с издательство, переработано и дополнено/ В.И. Ключев.– М.– Энергоатомиздат,2001. – 714с.
3. Присмотров Н.И. Электрический привод: учебное пособие/ Н.И. Присмотров, С.Н. Охапкин, Д.В. Ишутинов.– Киров: Издательство ВятГУ,2011. – 186с.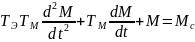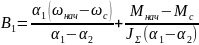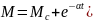