4.1.3. Полная и линеаризованная структурные схемы

В целом, рассматриваемая система электропривода представляет собой одноконтурную замкнутую САУ с последовательным корректирующим устройством (рис. 4.6).

Прямой канал полной структурной схемы САУ включает в себя: последовательное соединение звеньев сумматора У2 с входными воздействиями (задающим U_ЗАД и обратной связи U₁) и выходным воздействием U₂; коррекции У1 со входом U₂ и выходом U₃; тиристорного преобразователя, состоящего из инерционного звена 1-го порядка с коэффициентом усиления, равным единице, и безынерционного нелинейного звена с графическим изображением статической характеристики преобразователя (входным воздействием преобразователя служит U_з, а выходным – U_d) ; электродвигателя с указан­ными выше воздействиями U_d, n, U_С, M_С.

Канал обратной связи состоит из усилительного звена тахогенератора ТГ с коэффициентам передачи K_ТГ, входным воздействием n и выходным U_ТГ и фильтра в виде инерционного звена 1-го поряд­ка.

Рис. 4.6. Структурная схема САУ

Линеаризованная структурная схема САУ (рис.4.7) может быть составлена, если пол­ные переменные Х (U_ЗАД, U₂, U₃, U_d, U_С, I, M, M_С, n, U_ТГ, U₁) представить в виде суммы Х_A+X, где Х_A – значения переменных в рабочей точке А статических характеристик звеньев.

После сокращения статических составляющих в правой и левой час­ти уравнений звеньев линеаризованные структурные схемы звеньев отразят зависимость между приращениями выходных и входных переменных (U_ЗАД, U₂, …, U₁). Форма записи передаточных функ­ций линейных звеньев при этом не изменяется, а статические характеристики нелинейных безынерционных звеньев будут представлены в виде коэффициентов динамической линеаризации в рабочей точке.

Рис. 4.7. Структурная схема САУ с коэффициентом динамической линеаризации

4.1.4. Определение численных значений коэффициентов связи и постоянных времени неизменяемой части системы

Найдём сопротивление якоря двигателя

(Ом). (4.1.8)

Электромагнитная постоянная времени якорной цепи

. (4.1.9)

Конструктивный коэффициент электродвигателя С_Е рассчитывается по уравнению баланса напряжений якоря двигателя в установившемся номинальном режиме .

Тогда

. (4.1.10)

Найдём коэффициент передачи двигателя

. (4.1.11)

Электромеханическая постоянная времени двигателя

. (4.1.12)

Сравнивая передаточные функции электродвигателя по задающему воздействию и колебательного звена, можно определить коэффициент затухания:

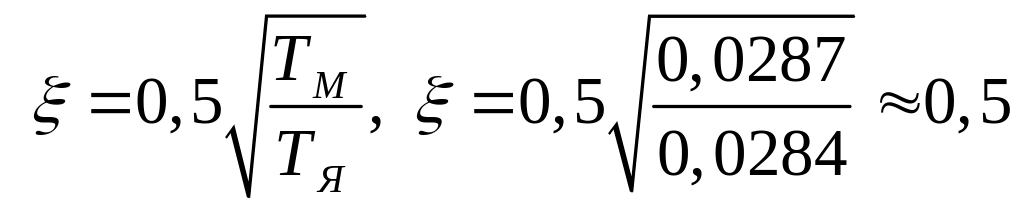. (4.1.13)

Если коэффициент демпфирования 0<<1 , то двигатель можно представить колебательным звеном, что и было сделано в п. 4.1.2. Собственная частота колебаний двигателя

. (4.1.14)

Из графической зависимости U_d(U₃), по данным табл. 1, постро­енной в одинаковом масштабе по обеим осям, определяется коэффициент k_П динамической линеаризации статической характеристики тиристорного преобразователя. или графически k_П равен тангенсу угла наклона касательной, проведенной к статической характеристике в рабочей точке А. Рабочая точка А определяется значением выпрямленного напряжения U_d|_A, в режиме идеального холостого хода электродвигателя. Значение k_П определяется в трех рабочих точках:

– k_{П min} при минимальном значении U_d в заданном диапазоне регулирования

D=10, т. е. U_{d min}= U_Н/D = 22(В); k_{П min} = 6,33; (4.1.15)

– k_{П max} – в точке с максимальным наклоном статической ха­рактеристики,

k_{П max} = 11; (4.1.16)

– k_{П ЗАД} при заданном значении выпрямленного напряжения

U_{d ЗАД} = С_Еn_ЗАД ; U_{d ЗАД}=1,98842 =83,5(В); k_{П ЗАД} =10,6; (4.1.17)

используется для построения ЛАЧХ САУ в заданном рабочем режиме.

Коэффициент момента равен

. (4.1.18)

Рис. 4.8. Статическая характеристика ТП