2 Розв’язування задач різними способами я засіб розвитку мислення школярів.

Сучасні вимоги щодо підвищення загального математичного рівня розвитку школярів молодших класів реалізується завдяки найважливішому із методів роботи – розв’язування задач різними арифметичними способами. Ця робота привчає дітей самостійно висувати гіпотези і перевіряти їх, порівнювати результати, доходити висновків, а головне, вона вчить мислити.

Вироблення звички шукати інший варіант розв’язування дуже важливе для майбутньої творчої, зокрема наукової діяльності, а саме вміння знаходити неординарні шляхи вирішення проблеми, і це забезпечує успіх у будь – якій справі.

Керівна роль вчителя під час пошуку інших варіантів розв’язання дуже важлива. Він сам повинен добре розв’язувати задачі, знати наперед, скількома способами можна знайти відповідь у кожній з них, ефективно використовувати при цьому час уроку.

Як правило, пошуки різних способів розв’язування дуже зацікавлюють учнів, особливо здібних до математики.

Поки вчитель розв’язує задачу 1 способом з рештою класу, здібні до математики діти вже встигають знайти кілька інших способів.

Розв’язування задач різними способами веде до розвитку і вміння всебічно аналізувати задану задачу.

Пошук іншого способу розв’язування приводить до встановлення нових зв’язків між величинами або використання відомих зв’язків у нових умовах.

Слід наголосити, що розв’язання, які відрізняються між собою лише порядком дій, не є різними.

М.В.Богданович у своїй книзі «Методика розв’язування задачв початковій школі» пропонує таку класифікацію різних способів розв’язання задач. Він розглядає способи розв’язування на такій задачі:

У юнната були кроля і індики. Всього у цих кролів і індиків було по 10 голів і 26 ніг. Скільки кролів і індиків було в юнната?

1. Спосіб випробування (спосіб проб і помилок)

Всього тварин 10. індиками вони всі бути не можуть, бо тоді б у них було б усього 20 ніг. Кролями теж всі не можуть бути, бо тоді б ніг було 40. будемо випробовувати:

Число кролів	Число індиків	Число ніг
1	9	22
2	8	24
3	7	26

Числа 3 і 7 підходять. У юнната було 3 кролі і 7 індиків.

2. Спосіб оригінальної здогадки

Уяві, що всі кролі стали на задні ноги, а кожен індик на 1. в такій позі були б зайняті половина всіх ніг, тобто 13. це на три більше, ніж всього було голів. Отже кролів було 3.

3. Спосіб припущення

Припустимо, що були самі індики. Тоді б ніг було тільки 20.Це на 6 менше, ніж було насправді. При заміні одного індика на кроля, тоді ніг збільшується на 2. отже, число кролів буде дорівнювати частці чисел 6 і 2 (6:2=3)

4. Алгебрагічний спосіб

Х - число кролів

(10-х) – число індиків

4х + 2(10-х)=26

2х+20=26

2х=6

Х=3

5. Узагальнений спосіб.Розглянемо задачу в загальному вигляді. Нехай число голів було п , а число ніг к. Позначимо кролів через х, а число індиків через у. дістанемо таку систему рівнянь.

х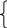 +у=п

4х+2у=к

Звідки х=к/2-п

В даному разі

26:2-10=3.

Кожен з розглянутих способів має свої переваги:

Метод проб і помилок готує до розуміння і застосування методу послідовних наближень, він широко використовується в науці.

Спосіб оригінальної догадки потребує образності та оригінальності мислення, вміння уявити реальну ситуацію так, щоб на першому плані були істотні ознаки розв’язуваного об’єкта.

Спосіб припущення ілюструє один з типових способі розв’язування алгебрагічної задачі.

Алгебрагічний спосіб та спосіб узагальнення свідчать про ефективність застосування алгебри.

Ознайомлення з різними способами розв’язування задачі здійснюється вже у другому класі.

Задача: У хлопчика бууло 8 білих кролів і 7 чорних. 5 чорних кролів він передав шкільній кролефермі. Скільки кролів стало у хлопчика?

I спосіб

1. Скільки у хлопчика всього кролів?

2. Скільки у хлопчика стало кролів?

II спосіб

1. Скільки залишилося чорних кролів?

2. Скільки у хлопчика стало кролів?

Задача

На льотному полі було 12 літаків. У політ вирушило 2 літаки, а потім ще 3. Скільки літаків залишилося на полі?

Поясни розв’язання кожним способом:

I спосіб

1) 2+3=5 (л)

2) 12-5=7 (л)

II спосіб

3. 12-2=10 (л)

4. 10-3=7 (л)

Задача .У ящику було 12 кг цибулі. За перший день витратили 4 кг цибулі, а за другий 5 кг. Скільки кілограмів цибулі залишилося в ящику?

I спосіб

1) Скільки кілограмів цибулі залишилося після першого дня продажу?

2) Скільки кілограмів цибулі залишилося після другого дня продажу?

II спосіб

1) Скільки кілограмів цибулі продали першого і другого дня?

2) Скільки кілограмів цибулі залишилося після двох днів продажу?

4 клас

Задача: Школярі зібрали з одного поля 1540 кг. Картоплі, причому 12 школярів зібрали по 75 кг кожний, а всі інші по 80 кг кожний. Скільки всього школярів збирали картоплю?

I спосіб

1. Скільки картоплі зібрали 12 школярів?

75*12=900 (кг)

2. Скільки картоплі зібрали ті, хто збирав по 80 кг кожний?

1540-900=640 (кг)

3. Скільки всього школярів збирали картоплю?

12+8=20 (шт)

Відповідь: 20 школярів.

II спосіб

Припустимо, що всі школярі збирали по 800 кг картоплі.

1. На скільки більше збирав би кожний із школярів?

80-75=5 (кг)

2. На скільки більше картоплі зібрали б усі 12 школярів?

5*12=60 (кг)

3. Скільки б усього зібрали б картоплі за припущенням?

1540+60=1600 (кг)

4. Скільки всього школярів збирали картоплю?

1600:80=20 (шк.)

Відповідь: 20 школярів.

III спосіб

Припустимо, що школярів, котрі збирали по 80 кг картоплі кожний було стільки ж, скільки й тих, кожний з яких збирав по 75 кг, тобто 12.

Скільки б усього зібрали б картоплі за припущенням?

(75+80)*12=1860 (кг)

На скільки більше картоплі зібрали б за припущенням, ніж насправді?

1860-1540=320 (кг)

Скільки школярів зібрали б ці 320 кг?

320:80=4 (шк.)

Скільки школярів насправді збирали по 80 кг картоплі?

12-4=8 (шк.)

Скільки всього школярів збирали картоплю?

12+8=20 (шк.)

Відповідь: 20 школярів.

IV спосіб

Припустимо, що картоплю збирали 25 чоловік.

1. Скільки було б тих, хто збирав по 80 кг картоплі?

25-12=13 (шк.)

2. Скільки картоплі зібрали б ці 13 школярів?

80*13=1040 (кг)

3. Скільки картоплі зібрали 12 школярів?

75*12=900 (кг)

4. Скільки за припущенням зібрали б картоплі всі учні?

900+1040=1940 (кг)

5. На скільки більше картоплі зібрали всі школярі за припущенням, ніж насправді?

1940-1540=400 (кг)

6. Скільки школярів, збираючи по 80 кг, спроможні заготовити таку кількість картоплі?

400:80=5 (шк.)

7. Скільки школярів насправді збирало по 80 кг картоплі?

13-5=8 (шк.)

8. Скільки всього школярів збирали картоплю?

8+12=20 (шк.)

Відповідь: 20 школярів.

Розв’язування задач різними способами активізує різні аспекти математичної діяльності учнів.

У початкових класах прийом розв’язання задач різними способами навчально – пропедевтичний характер.

Треба з’ясувати можливість розв’язання задач різними способами; застосувати їх при ілюстрації деяких властивостей арифметичних дій, наприклад, додаванні суми до числа, відніманні суми від числа, розподільній властивості множення чи ділення відносно додавання чи віднімання; організувати самостійне розв’язування учнями різними способами таких задач, в яких кожен із способів добре інтерпретується життєвою ситуацією чи практичним виконанням.