2.3 Определение достоверности расчета статистических

параметров ряда наблюдений.

Определяют достоверность расчета параметров ряда и по относительным среднеквадратическим ошибкам:

для нормы стока 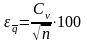, %; (2.7)

для коэффициента вариации (изменчивости)

. (2.8)

По СП 33-101-2003 расчетный параметр считается достоверным, а период наблюдений достаточным, если относительная среднеквадратическая ошибка этого параметра не превышает 10%.

Так как для достоверного расчета коэффициента асимметрии С_s по формуле (2.4) необходим ряд с числом лет наблюдений N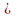 100 лет, определение ошибки этого параметра не имеет смысла, коэффициент асимметрии уточняют методом подбора.

Например:

По формулам (2.7) и (2.8) вычисляют относительные среднеквадратические ошибки:

нормы стока

коэффициента вариации

.

Так как и более 10%, то норма стока =2,53 л/(с·км²) и коэффициент вариации (изменчивости) C_v=0,42 не достоверны, ряд наблюдений надо было бы удлинить. Условно считают эти параметры достоверными. Так как n=20 « 100 лет, то вычисленное значение коэффициента асимметрии С_s=0,74 является не достоверным, предварительным, его значение уточняют методом подбора аналитической кривой обеспеченности стока к эмпирическим точкам.

2.4.Уточнение значения коэффициента асимметрии методом подбора.

Метод подбора выполняют графически.

Смысл метода состоит в том, что к эмпирическим точкам, которые графически представляют ряд наблюдений, подбирают аналитическую кривую обеспеченности стока из нескольких кривых при одном и том же вычисленном значении С_v и разных значениях С_s.

За аналитические кривые обеспеченности по рекомендации СП 33-101[8] приняты кривые трехпараметрического гамма- распределения. Ординаты этих кривых для разных значений С_s приведены в таблице «Определение расчетных характеристик речного стока». Значения коэффициента асимметрии для этих кривых выражено в долях к С_v: 0,5 С_v; 1С_v; 1,5 С_v и т.д. В первую очередь имеет смысл проверить два значения С_s:

1. С_s=2 С_v, так как 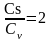- наиболее характерное значение для годового сток рек Европейской части России;

2. Значение, близкое к предварительному, вычисленному по формуле (2.4).

На один рисунок наносят эмпирические точки и аналитические кривые обеспеченности стока. Кривую обеспеченности стока, которая ближе подходит к эмпирическим точкам, выбирают за расчетную принимая значение C_s этой кривой за окончательное для ряда наблюдений.

Например:

На рисунок 3 (миллиметровая бумага формата А4) по данным таблицы 2.2, графы 6 и 10, наносят эмпирические точки.

Принимают два значения коэффициента асимметрии:

1. С_s=2C_v;

2. близкое к предварительному по формуле (2.4) С_s=0,74. Определяют отношение . Видно, что нужно тоже принять , но так как это значение уже принято в первом случае, берут другое близкое значение (в меньшую сторону) , то есть С_s=1,5C_v. В таблицу 2.3 из таблицы выписывают ординаты аналитических кривых при C_v=0,42 и С_s=2 C_v и С_s=1,5 C_v.

Таблица 2.3 – Ординаты аналитических кривых обеспеченности годового стока р.Северский Донец, г.Змиев при C_v=0,42

Сs	Ординаты Кр% для обеспеченностей Р, %
	0,1	1	5	10	25	40	50	60	75	80	90	95	97	99	99,9
Сs=2Cv	2,81	2,23	1,78	1,57	1,24	1,05	0,94	0,84	0,69	0,64	0,51	0,43	0,37	0,28	0,18
Сs=1,5Cv	2,64	2,16	1,76	1,57	1,26	1,06	0,95	0,85	0,69	0,63	0,50	0,40	0,34	0,25	-

На рисунке 3 строят две аналитические кривые обеспеченности стока при C_v=0,42, а С_s=2·C_v, С_s=1,5· C_v. За расчетную кривую обеспеченности годового стока принимают кривую при C_v=0,42 и С_s=2· C_v, так как эта кривая ближе подходит к эмпирическим точкам в верхней и нижней частях, а в средней части эмпирические точки располагаются более симметрично к этой кривой. (Следует отметить, для данного примера выбор расчетной кривой является формальным, так как значения С_s=2· C_v и С_s=1,5· C_v близки и кривые мало отличаются друг от друга).

В результате расчетов приняты следующие значения основных статистических параметров годового ряда наблюдений (кривой обеспеченности):

норма стока в виде модуля стока

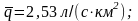
коэффициент вариации (изменчивости) C_v=0,42;

коэффициент асимметрии С_s=2· C_v.