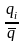- •Климатология, метеорология и гидрология
- •Климатология, метеорология и гидрология
- •280401.65- «Мелиорация, рекультивация и охрана земель»,
- •280402.65 – «Природоохранное обустройство территорий»
- •280402.65 – «Природоохранное обустройство территорий»
- •Гидрометеорологические расчеты
- •2. Расчет годового стока при наличии данных наблюдений
- •3. Определить максимальный расход воды при отсутствии данных наблюдений для IV класса сооружений
- •1.Расчет климатических и метеорологических факторов
- •1.1. Построение климатограммы по годовому ходу температуры воздуха.
- •1.2. Определение характеристик влажности воздуха.
- •1.3 Построение «розы ветров»
- •2.1 Общие указания
- •2.2 Определение основных статистических параметров ряда наблюдений (кривой обеспеченности) методом моментов
- •2.3 Определение достоверности расчета статистических
- •2.4.Уточнение значения коэффициента асимметрии методом подбора.
- •2.5 Определение характеристик годового стока разных обеспеченностей, повторяемости и степени водности
- •3 Определение максимального расхода воды при отсутствии данных гидрометрических наблюдений
2.2 Определение основных статистических параметров ряда наблюдений (кривой обеспеченности) методом моментов
По ряду наблюдений в виде модулей стока определяют основные статистические параметры ряда:
норму
стока в виде модуля
 ;
(2.2)
;
(2.2)
коэффициент
вариации
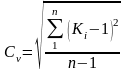 ;
(2.3)
;
(2.3)
коэффициент
асимметрии
 ,
(2.4)
,
(2.4)
где
 -
модульный коэффициент,
-
модульный коэффициент,
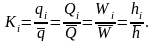 (2.5)
(2.5)
Расчет
ведут в виде таблицы 2.2. Исходный ряд
наблюдений в виде среднегодовых модулей
стока располагают в порядке убывания
(ранжируют) и вычисляют сумму членов
ряда
 .
По формуле (2.2) вычисляют норму стока
,
а затем модульные коэффициенты
по убывающему ряду
.
По формуле (2.2) вычисляют норму стока
,
а затем модульные коэффициенты
по убывающему ряду
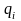 ,
используя выражение (2.5). Проверяют
выполнение условия:
,
используя выражение (2.5). Проверяют
выполнение условия:

Таблица 2.2 – Определение основных статистических параметров ряда годового стока р.Северский Донец, створ г.Змиев
Ряд наблюдений |
Статистическая обработка |
Эмпирическая
обеспеченность
|
||||||||
Условный год |
Среднегодовые модули стока qi, л/(с·км2) |
Порядковый номер mi |
Условный год |
Среднегодовые модули стока в убывающем порядке qi, л/(с·км2)
|
Модульный
коэффициент Кi= |
Отклонение от среднего (Кi-1) |
(Кi-1)2 |
(Кi-1)3 |
||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
1 |
1,50 |
1 |
16 |
4,84 |
1,91 |
0,91 |
0,828 |
0,754 |
5,9 |
|
2 |
1,85 |
2 |
15 |
4,16 |
1,64 |
0,64 |
0,410 |
0,262 |
11,8 |
|
3 |
1,84 |
3 |
6 |
3,52 |
1,39 |
0,39 |
0,152 |
0,059 |
17,6 |
|
4 |
3,29 |
4 |
4 |
3,29 |
1,30 |
0,30 |
0,090 |
0,027 |
23,5 |
|
5 |
1,78 |
5 |
14 |
3,28 |
1,30 |
0,30 |
0,090 |
0,027 |
29,4 |
|
6 |
3,52 |
6 |
13 |
3,16 |
1,25 |
0,25 |
0,062 |
0,016 |
35,3 |
|
7 |
2,71 |
7 |
7 |
2,71 |
1,07 |
0,07 |
0,005 |
0,000 |
41,2 |
|
8 |
1,30 |
8 |
10 |
2,23 |
0,88 |
-0,12 |
0,014 |
-0,002 |
47,1 |
|
9 |
2,07 |
9 |
9 |
2,07 |
0,82 |
-0,18 |
0,032 |
-0,006 |
52,9 |
|
10 |
2,23 |
10 |
2 |
1,85 |
0,73 |
-0,27 |
0,073 |
-0,020 |
58,8 |
|
11 |
1,28 |
11 |
3 |
1,84 |
0,73 |
-0,27 |
0,073 |
-0,020 |
64,7 |
|
12 |
1,73 |
12 |
5 |
1,78 |
0,70 |
-0,30 |
0,090 |
-0,027 |
70,6 |
|
13 |
3,16 |
13 |
12 |
1,73 |
0,68 |
-0,32 |
0,102 |
-0,033 |
76,5 |
|
14 |
3,28 |
14 |
1 |
1,50 |
0,59 |
-0,41 |
0,168 |
-0,069 |
82,4 |
|
15 |
4,16 |
15 |
8 |
1,30 |
0,51 |
-0,49 |
0,240 |
-0,118 |
88,2 |
|
16 |
4,84 |
16 |
11 |
1,28 |
0,50 |
-0,50 |
0,250 |
-0,125 |
94,1 |
|
Сумма |
40,54 |
16,00 |
0,00 |
2,679 |
+1,145 -0,420 +0,725 |
|
||||
Если
получается невязка в пределах допустимого
(0,1), ее разбрасывают с обратным знаком,
добиваясь выполнения этого условия.
Затем находят отклонения каждого члена
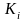 от среднего
от среднего
 то есть
то есть
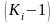 ,
и сумму этих отклонений:
,
и сумму этих отклонений:
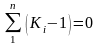 .
Отклонение от среднего значения возводят
в квадрат
.
Отклонение от среднего значения возводят
в квадрат
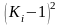 и в куб
и в куб
 и вычисляют суммы:
и вычисляют суммы:
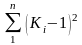 и
и
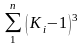 .
Эти суммы необходимы для расчета по
формулам (2.3) и (2.4) коэффициентов
изменчивости и асимметрии.
.
Эти суммы необходимы для расчета по
формулам (2.3) и (2.4) коэффициентов
изменчивости и асимметрии.
Эмпирическую обеспеченность члена убывающего ряда вычисляют по формуле Крицкого-Менкеля:
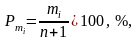 (2.6)
(2.6)
где mi- порядковый номер.
Например:
Исходный
ряд наблюдений в виде среднегодовых
модуле стока
за условно достаточный период n=16
лет берут из исходных данных. Выписывают
этот ряд в графу 2 таблицы 2.2. В графе 5
располагают модули стока в убывающем
порядке и в графе 4 выписывают номер
условного года. Вычисляют сумму членов
ряда
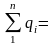 40,54
л/(с·км2).
По формуле (2.2) вычисляют норму стока
40,54
л/(с·км2).
По формуле (2.2) вычисляют норму стока
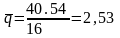 л/(с·км2).
Вычисляют модульные коэффициенты Кi
по убывающему ряду qi,
используя выражение (2.5), и результаты
выписывают в графу 6. Суммируют вычисленные
Кi:
л/(с·км2).
Вычисляют модульные коэффициенты Кi
по убывающему ряду qi,
используя выражение (2.5), и результаты
выписывают в графу 6. Суммируют вычисленные
Кi:
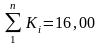 - невязка отсутствует. (При наличии
невязки ее разбрасывают, добиваясь
выполнения условия
- невязка отсутствует. (При наличии
невязки ее разбрасывают, добиваясь
выполнения условия
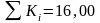 ).
).
В
графе 7 вычисляют (Кi-1)
и сумму:
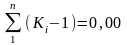 -
проверка выполнена. В графе 8 вычисляют
квадраты отклонений и их сумму:
-
проверка выполнена. В графе 8 вычисляют
квадраты отклонений и их сумму:
 По формуле (2.3) вычисляют коэффициент
вариации
По формуле (2.3) вычисляют коэффициент
вариации
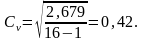
В
графе 9 вычисляют кубы отклонений и их
сумму:
 По формуле (2.4) вычисляют коэффициент
асимметрии
По формуле (2.4) вычисляют коэффициент
асимметрии
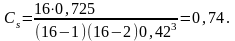
По формуле (2.6) в графу 10 вычисляют для каждого порядкового номера mi эмпирическую обеспеченность:
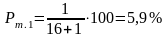 ;
;
 ;
;
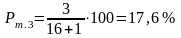
и т.д.

 ,%
,%