4.1.3. Обчислення кількости тепла за істинною і середньою теплоємностями

Означення істинної теплоємности використовується для обчислення кількости тепла. З (4.9) випливає, що

δq_x = с_xdT. (4.13)

Для кінцевого процесу х сумарна кількість тепла дорівнює:

q_x,1→2 = _, (4.14)

де t – температура за шкалою Цельсія.

Якщо с_х не залежить від температури (рис.4.2), то площа F(t₁,1,2,t₂) чисельно дорівнює кількости тепла процесу х:

q_x,1→2 = с_х (t₂ – t₁). (4.15)

Що є, безумовно, ідеалізацією. В цьому випадку поняття істинної і середньої теплоємностей співпадають.

с

с₁ = с₂ 1 2

F

t₁ t₂ t

Рис.4.2. Залежність теплоємности від температури при c_х (t) = const

Якщо c_х залежить від температури (рис.4.3), то площа F(t₁,1,2,t₂) чисельно дорівнює кількости тепла процесу х:

q_x,1→2= .

І для того, щоб обчислити цей інтеграл, необхідно мати аналітичний вираз с_х = f (t).

Результати експерименту по визначенню теплоємности апроксимують многочленом k-го порядку:

c_х=b₀+b₁t + b₁₁t² + b₁₁₁t³ + …. + b₁…₁ t^k, (4.16)

або c_х=b₀+b₁t + b₁₁ t^-2 + b₁₁₁ t^-3 + …+ b_1…1 t ^{– k}, (4.17)

де b₀ ,b₁ , b₁₁ .... – емпіричні коефіцієнти, які мають певні значення для даного інтервалу температур.

с

2

1

2

b

a

1

t₁ t₂ t

Рис.4.3. Залежність теплоємности від температури при с_х = var ≠ const:

1− лінійна залежність; 2− нелінійна залежність

Часто достатньо наближення другого порядку:

c_х=b₀+ b₁t + b₁₁t² ; (4.18)

c_х=b₀+b₁t + b₁₁t ^-2, (4.19)

або іноді і першого порядку:

c_х=b₀+b₁t. (4.20)

Для (4.20) b₀ і b₁ можна визначити графічно.

Кількість тепла, що витрачається на нагрів n молей речовини від t₁ до t₂, визначається співвідношеннями:

з (4.18)

;

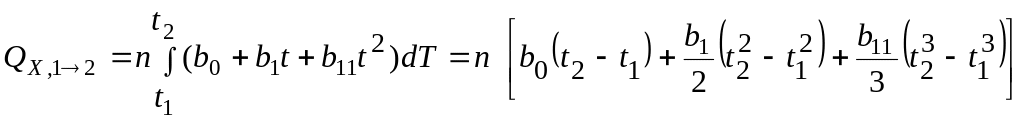з (4. 19)

Q_x,1→2 ;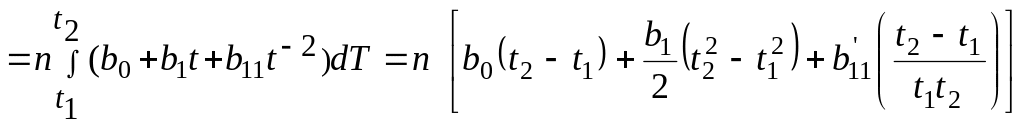

з (4.20) Q_x,1→2= .

Але часто аналітичний вигляд функції с_х = f(t) невідомий, тоді для обчислення кількости тепла користуються означенням середньої теплоємности , яка визначена для кінцевого інтервалу температур (рис. 4.3):

с_mx . (4.21)

Вираз (4.21) характеризує в загальному вигляді зв’язок між середньою та істинною теплоємностями. Тоді,

q_{x, 1→2} = с_{m x} . (4.22)

Зауважимо, що питомі теплоємности (масова, об’ємна, мольна) визначені як для істинної, так і середньої теплоємностей.

Експериментально знайдені (або теоретично розраховані) величини середніх теплоємностей можуть бути зведені в таблиці (табульовані), але при цьому необхідний перебір всіх сполучень температур. Тому, при табулюванні необхідно задатися початковою (вихідною, реперною) точкою, наприклад t_о = 0^оC; t_а = 0,01^оC; t = 25^оC.

Знайдемо співвідношення істинної і середньої теплоємностей за допомогою рівнянь (4.14), (4.21), (4.22):

(4.23)

.

Таким чином, рівняння (4.23) дозволяє за табличними даними розрахувати значення середньої теплоємности для будь-якого інтервалу температур. Тоді, з (4.22) витікає формула для розрахунку тепла за допомогою середньої теплоємности:

q_{x, 1→2}= с_mx . (4.24)