2. Ошибки, вызываемые квантованием коэффициентов цифрового фильтра.

Идеальная (расчётная) системная функция цифрового фильтра:

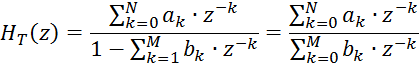
где , .

Квантованные коэффициенты:

где и – погрешности квантования независимой случайной величины.

Системная функция реального цифрового фильтра:

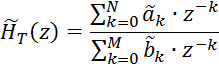
Алгоритм работы идеального цифрового фильтра:

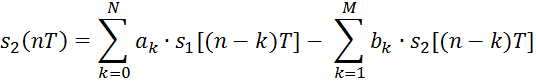
Алгоритм работы реального цифрового фильтра:

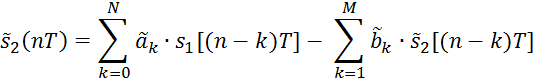
Обозначим ошибку из-за квантования коэффициентов

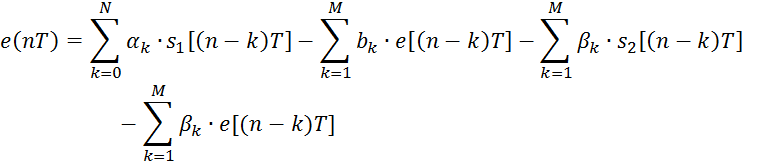
Можно считать, что слагаемое – бесконечно малая величина, тогда:

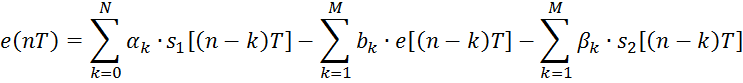
или

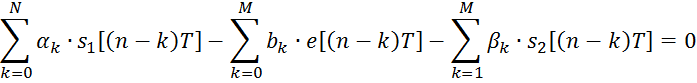
Возьмём Z-преобразование от левой части этого уравнения:

где

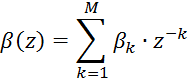
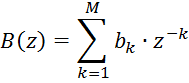
B(z) – знаменатель системной функции идеального цифрового фильтра;

S₁(z) – Z-преобразование воздействия;

S₂(z) – Z-преобразование отклика идеального цифрового фильтра;

E(z) – Z-преобразование ошибки цифрового фильтра.

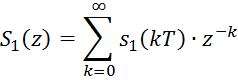
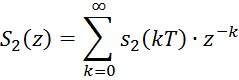
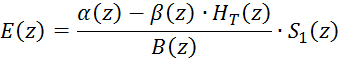
Полученные выражения позволяют изобразить модель цифрового фильтра с учётом ошибок, вызванных квантованием коэффициентов:

Здесь – Z-преобразование отклика реального фильтра.

Пользуясь этой моделью и зная статистические свойства погрешностей и , можно оценить среднеквадратическое отклонение частотной характеристики реального фильтра от частотной характеристики идеального фильтра.

В известной литературе показано, что в нерекурсивных фильтрах небольшие искажения коэффициентов из-за квантования, приводят к незначительным искажениям частотных характеристик, например, происходит небольшое увеличение пульсаций областей пропускания и задерживания фильтра. Однако, если фильтр должен иметь очень крутой спад АЧХ, то даже малые изменения коэффициентов могут привести к заметным искажениям АЧХ.

В рекурсивных фильтрах (особенно высокого порядка) округление коэффициентов гораздо сильнее сказывается на частотной характеристике фильтра. Объясняется это тем, что коэффициенты связаны с частотной характеристикой нелинейно. Даже небольшие изменения коэффициентов могут привести к заметным изменениям АЧХ (особенно при наличии крутых спадов).

Заметим, что для уменьшения искажений, вызванных квантованием коэффициентов, рекомендуется переход от прямой формы построения цифрового фильтра к последовательной (секционной), когда цифровой фильтр представляет собой последовательное включение звеньев не высокого порядка (1 или 2).

3. Округление результатов промежуточных вычислений при цифровой фильтрации.

Источником шума округления при цифровой фильтрации является округление результатов умножения промежуточных переменных на коэффициент.

Если оба перемножаемых числа имеют q-разрядное представление, то результат будет иметь 2 q-разряда, поэтому приходится округлять результат умножения до q-разрядов.

Этот процесс можно отразить моделью:

– шум округления;

По аналогии с шумами АЦП дисперсию этого шума можно записать в виде:

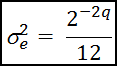
где q – разрядность представления чисел;

Пример: КИХ – фильтр N-го порядка.

Обычно считают, что любые два источника шума в ЦФ некоррелированы, а шум от каждого источника некоррелирован с входным сигналом. Тогда дисперсия шума округления на выходе фильтра может быть найдена как сумма дисперсий шума, вызываемого каждым источником в отдельности.