1.15. Быстрое преобразование Фурье (бпф)

Сущность быстрого преобразования Фурье заключается в разбиении исходной последовательности отсчетов {s(nT)} объемом N (N считается равным 2^m) на две последовательности (четную и нечетную), для каждой из которых вычисляется ДПФ, а результаты объединяются. Можно показать, что при таком однократном прореживании по времени получается сокращение числа арифметических операций, необходимых для нахождения отклика, примерно в 2 раза.

При необходимости прореживание по времени можно проводить многократно, пока в каждой последовательности останутся по 2 отсчета (тогда спектральные коэффициенты находятся путем сложения и вычитания отсчетов).

При таком многократном прореживании получается экономия в числе арифметических операций для нахождения отклика примерно в N / log₂N раз.

Например, при N=2¹⁰=1024, обычное ДПФ требует N² 10⁶ арифметических операций, в то время как при БПФ их требуется примерно в 100 раз меньше.

Заметим, что существенная экономия получается лишь при большом N.

Возможен и другой алгоритм реализации БПФ, называемый прореживанием по частоте.

Аналогично алгоритмам реализации прямого БПФ существуют алгоритмы реализации обратного БПФ.

1.16 Структурная схема линейной дискретной фильтрации на основе дпф (бпф)

На основе рассмотренного в параграфе 5 спектрального метода анализа прохождения сигнала через ДФ можно предложить следующую структурную схему линейной дискретной фильтрации (рис. 21.)

При этом предполагается, что через интервал времени Т набор дискретных отсчетов s₁(nT), поступающих на блок прямого ДПФ (БПФ) сдвигается на такт (то есть обновляется).

Это обеспечивает работу фильтра в реальном масштабе времени. Такой метод фильтрации широко применяется при использовании современных быстродействующих универсальных и специализированных ЭВМ.

Раздел 2. Эффекты квантования при цифровой фильтрации.

1. Шум квантования, возникающий при аналого-цифровом преобразовании.

Аналого-цифровой преобразователь (АЦП) – предназначен для преобразования отсчётов воздействия из аналоговой формы в цифровую.

Отсчёты могут принимать лишь дискретные (квантованные) значения.

Будем считать, что при квантовании происходит округление значений отсчётов с шагом квантования .

Характеристика квантования в этом случае имеет вид:

Такое квантование приводит к ошибке. Сигнал ошибки представляет собой разность:

Воспользуемся моделью формирования отсчёта АЦП в виде:

– шум квантования.

Величина – есть случайная величина.

– математическое ожидание.

Дисперсия шума квантования:

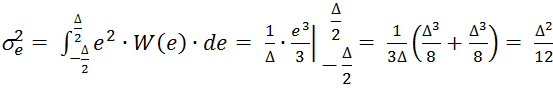
Число уровней квантования:

q – число двоичных разрядов АЦП.

Такая модель формирования отсчётов АЦП применяется лишь при достаточно большом количестве разрядов АЦП (q  5).

Чтобы найти дисперсию шума на выходе цифрового фильтра, вызванную эффектом квантования отсчётов воздействия, можно с учётом независимости отсчётов сигнала и отсчётов шума найти отклик фильтра только на отсчёты шума.

Например для нерекурсивного фильтра алгоритм работы такой:

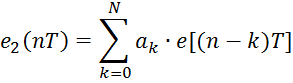
Если считать отсчёты шумов квантования некоррелированными, то дисперсию случайной величины можно найти как сумму дисперсий каждого слагаемого в правой части предыдущего выражения.