1.6. Частотные характеристики дискретныхлинейных фильтров.

Комплексный коэффициент передачи дискретного фильтра, записанный в общем (для рекурсивного и нерекурсивного) виде:

является периодической функцией частоты.

Представив

можно ввести понятия АЧХ и ФЧХ дискретного фильтра

которые тоже являются периодическими функциями частоты.

Рассмотрим два примера:

Пример 1. Нерекурсивный дискретный фильтр.

Рис. 15.

Очевидно, что частота повторения

При а₀=1 и а₁=1 АЧХ и ФЧХ дискретного фильтра соответственно имеют вид:

Рис. 16.

При а₁= - 1, АЧХ и ФЧХ смещаются по оси частот на π/ Т.

Как видим, рассматриваемый фильтр при и a₁=1 может рассматриваться как ФНЧ, причем его ФЧХ линейна, частотные характеристики являются периодическими функциями с периодом ω_T=2π / T. В отличие от аналоговых фильтров частотные характеристики дискретных фильтров можно задавать лишь в интервале частот

Путем изменения времени задержки Т и весовых коэффициентов а₀ и а₁ можно добиться перестройки фильтра в широких пределах.

Пример 2. Рекурсивный фильтр.

В качестве примера возьмем фильтр, изображенный на рис. 14. Его комплексный коэффициент передачи

При а₀=1 и b₁=1 АЧХ имеет вид (рис. 17)

Рис. 17.

При b₁= - 1 АЧХ смещается по оси частот на π / T.

ФЧХ в примере 2 похожа на ФЧХ из примера 1, если а₁= - 1 и знак фазы поменять на обратный.

1.7. Применение z-преобразования для анализа дискретных сигналов и фильтров.

Основные выражения, описывающие характеристики дискретных сигналов и фильтров, содержат трансцендентные функции вида е^-kpT или е^-jkωT , что существенно усложняет анализ прохождения сигналов через дискретные фильтры.

Для упрощения можно воспользоваться так называемым Z-преобразованием

Z=e^pT

или

Тогда изображение дискретного сигнала

преобразуется в алгебраическое выражение вида

Передаточная функция ДФ также упрощается:

Принято называть (z) – системная функция

На структурных схемах соответственно идеальный элемент задержки на время kT изображается в виде .

Существует и обратное z-преобразование, при котором находятся временные характеристики

1.8. Анализ прохождения сигнала через дискретный фильтр временным методом.

Если известен алгоритм работы или структурная схем ДФ и известны отсчеты воздействия фильтра, то отклик линейного дискретного фильтра может быть легко найден с помощью принципа суперпозиции: находятся отдельно отклики на каждый отсчет воздействия, а результаты складываются.

Так, для нерекурсивного фильтра)

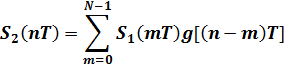
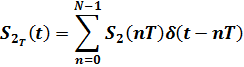
Для рекурсивного дискретного фильтра отклик находится аналогичным способом, но в общем случае за счет задержанной обратной связи, отклики на каждый отсчет воздействия имеют неограниченное число отсчетов (для устойчивой работы фильтра они должны постепенно уменьшаться).

Например, для рекурсивного фильтра

Простота анализа прохождения сигнала через ДФ временным методом является лишь кажущейся, так как с увеличением числа отсчетов N трудоемкость вычислений существенно возрастает. Действительно, для нахождения одного отсчета отклика требуется осуществить N операций умножения и N операций сложения. Даже если пренебречь более простыми операциями сложения, остается N операций умножения. Для нахождения отклика фильтра s_2Т(t) потребуется еще N умножений. В результате общая трудоемкость оценивается величиной N², при этом заметим, что для исключения искажений при вычислении дискретной свертки (16) под величиной N следует понимать сумму необходимого числа отсчетов воздействия N_s1 и необходимого числа отсчетов импульсной характеристики N_g, то есть

N = N_s1+ N_g

При анализе прохождения сложных сигналов с большой базой f_вT_c>>1 число арифметических операций для нахождения отклика ДФ становится настолько большим, что даже при использовании современной элементной базы вычисления в реальном масштабе времени становятся проблематичными.