4.7. Синтез узкополосного ких – фильтра нижних частот на основе децимации импульсной характеристики.
Наблюдаемый в ГФ эффект прореживания (децимации) ИХ напоминает эффект прореживания (децимации) отсчетов входного сигнала при вторичной дискретизации сигнала и может быть использован при синтезе узкополосного ЦФ.
Пусть
требуется синтезировать узкополосный
КИХ – фильтр нижних частот с заданными
свойствами частотной избирательности
(
,
,
,
α, β). Эти параметры определяют порядок
фильтра N и вычислительные затраты
(
.
Представим структуру такого фильтра в виде последовательно включенных гребенчатого (ЦФГ) и сглаживающего (ЦСФ) цифровых фильтров (рис.8).
рис.8
При
этом АЧХ ГФ должна в диапазоне рабочих
частот
содержать составляющие, повторяющиеся
с периодом 
и имеющие такие же свойства частотной
избирательности, как у синтезируемого
ФНЧ.
Если для ФНЧ заданы параметры избирательности , , , α и β , то однозначно определяется его порядок N.
Для ЦГФ выбирают такие же параметры:
Параметр для ЦГФ и ЦСФ, как показано в литературе, необходимо уменьшить в 2 раза.
ЦСФ
должен иметь такую АЧХ, чтобы выделять
основной лепесток из составляющих на
выходе ЦФГ. При этом не предъявляются
строгие требования к прямоугольности
его АЧХ, т.е. 
.
Следовательно при 
,
,
, 
порядок сглаживающего фильтра 
,
а частота 
должна удовлетворять условию 
.
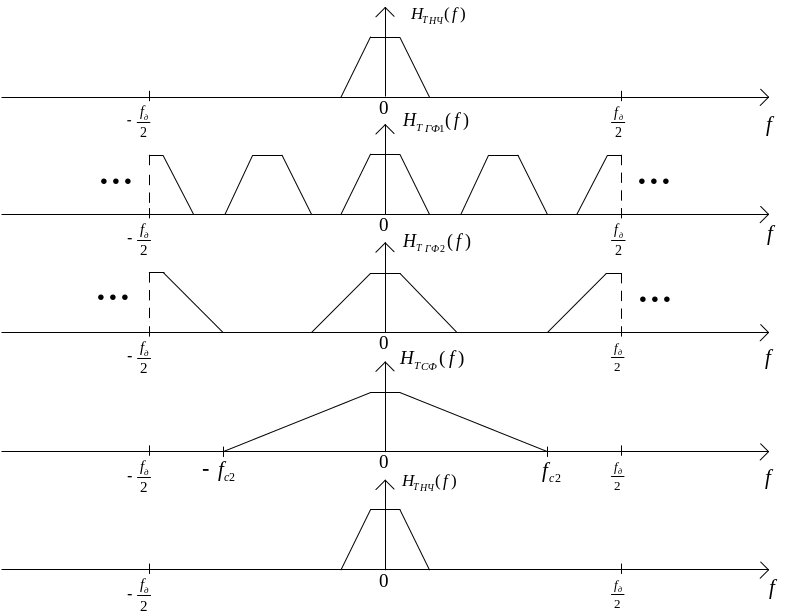
На рис.9 приведены АЧХ для исходного ФНЧ (а), гребенчатого фильтра (б) и сглаживающего фильтра (в).
рис.9
Заметим,
что при увеличении коэффициента децимации
ИХ мы будем вынуждены делать 
меньше, а это приведет к увеличению
коэффициента 
,
порядка СФ 
и, соответственно к увеличению
вычислительных затрат 
.
Оценим эффективность двухкаскадной реализации узкополосного КИХ – фильтра нижних частот по сравнению с прямой его реализацией, при одинаковом порядке фильтра N.
Во-первых: За счет прореживания ИХ, в двухкаскадном варианте уменьшается в – раз вычислительные затраты на реализацию ЦГФ.
Во-вторых: В отличии от методов использующих вторичную дискретизацию сигнала, двухкаскадная схема не вносит дополнительных шумов децимации и интерполяции (см.ранее).
В-третьих:
Важным достоинством такой реализации
узкополосного ЦФ является значительное
снижение уровня собственных шумов,
благодаря многократному уменьшению
числа операций умножения с округлением
результата ( в ЦГФ таких операций 
, а в ЦСФ порядок
).
Кроме того, в двухкаскадном варианте уменьшается объем памяти для хранения коэффициентов фильтра, что связано с уменьшение числа отсчетов ИХ. В то же время двухкаскадная форма реализации приводит к дополнительным вычислительным затратам в ЦСФ. Хотя они и не так велики ( ), поскольку к этому фильтру не предъявляются высокие требования к прямоугольности АЧХ, но появляются противоречия между требованиями к ЦГФ и требованиями ЦСФ.
Сущность
этих противоречий заключается в
следующем: С одной стороны, чем больше
коэффициент децимации
, тем больше вычислительные затраты на
реализацию ЦГФ. С другой стороны, с
увеличением 
ужесточаются
требования к ЦСФ.
В
известной литературе по ЦОС показано,
что при оптимальном согласовании
требований к ЦГФ и ЦСФ, можно добиться
максимальной экономии вычислительных
затрат по сравнению с обычным ЦФНЧ,
который определяется числом 
, где N- порядок синтезируемого фильтра.
При высоком порядке разрабатываемого
фильтра можно добиться выигрыша в
несколько десятков или сотни раз.
Если этого недостаточно, то возможна так называемая трехкаскадная схема построения узкополосного фильтра, когда ЦСФ реализуется путем последовательного соединения вспомогательного (дополнительного) ГФ и выходного СФ.
Т
ребования
к частотным характеристикам этих трех
фильтров можно определить по аналогии
с двухкаскадной схемой, но необходимо
принять:
При трехкаскадной форме построения узкополосного ЦФ получается дополнительный выигрыш в вычислительных затратах, по сравнению с двухкаскадной.
В принципе возможны четырехкаскадные и пятикаскадные формы реализации, но как показали результаты исследований, практически это мало что дает.
Содержание