2. Метод Крошье, Рабинер, Шелеви

Идея заключается в оптимизации числа ступеней децимации и интерполяции с произвольными коэффициентами децимации в каждой ступени с целью минимальных затрат.

В простейшем случае структурная схема такого КИХ – фильтра может быть двухступенчатой:

В этой схеме на ФНЧ₁, стоящей в дециматоре, не накладываются высокие требования к прямоугольности АЧХ. Он должен обеспечить граничную частоту соответствующую частоте дискретизации.

ω_д2 = ; α₁ << α ; N₁ ~ α₁ << N

В формирующем фильтре обеспечивается прямоугольность АЧХ, и поэтому в этом фильтре:

α₀ = α ; β₀ = β ; ω_д2 = ; N₀ = → выигрыш в ν раз.

4.4 Особенности временной дискретизации радиосигнала

До сих пор нами рассматривалась временная дискретизация и цифровая фильтрация низкочастотных сигналов (видео - сигналов). Если S(t) низкочастотный сигнал, спектр которого ограничен интервалом частот от –ω­_в до + ω­_в, то он полностью определяется своими отсчетами, взятыми через интервал T ≤ =

Радиосигнал: a(t) = A(t) cos [ω_нt + φ(t)] = A(t) cos ψ(t), где (1)

A(t) – огибающая радиосигнала;

ω_н - центральная частота радиосигнала (несущая);

φ(t) – фаза радиосигнала;

ψ(t) - полная фаза радиосигнала.

Выражение (1) не дает однозначного определения огибающей и фазы сигнала. Для однозначного определения этих понятий применяют прямое преобразование Гильберта (ППГ):

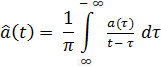
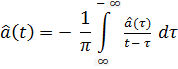
– обратное преобразование Гильберта (ОПГ),

Тогда A(t) = ,

ψ(t) = arctg ;

ω(t) = = ω_н + - мгновенная частота.

Благодаря преобразованию Гильберта определили ω_н, A(t), φ(t).

Для уменьшения искажений при прохождении радиосигнала через радио цепи относительная ширина радиосигнала должна быть много меньше единицы ( << 1), то есть радиосигнал должен быть узкополосным. Ширина спектра радиосигнала определяется шириной спектра управляющего (модулирующего) колебания S(t).

S_a(ω) – амплитудный спектр радиосигнала.

2 Δω_а ≈ 2 Δω , следовательно, наивысшая частота в спектре управляющего колебания Ω_max << ω_н .

S(t) – является медленноменяющимся колебание по сравнению с несущим колебанием.

Так огибающая A(t) и (или) фаза φ(t) повторяют закон изменения S(t), то они тоже являются медленноменяющимися колебаниями по сравнению с несущим колебанием. Это означает, что за период несущего колебания T = A(t) и φ(t) практически не меняются.

Если подойти к временной дискретизации радиосигнала формально, то исходя из наибольшей частоты в спектре радиосигнала ω_в = ω_н + Δω_a , нужно было бы выбрать интервал между отсчетами: T ≤ = = .

Однако, учитывая медленность изменения параметров радиосигнала, это нецелесообразно.

Чтобы правильно выбрать интервал дискретизации радиосигнала воспользуемся комплексным представлением радиосигнала:

Z (t) = a(t) + j (t) или

Z (t) = A(t)e ^jωн(t) , где

A (t) = A(t)e^jφ(t) – комплексная огибающая радиосигнала

S_z (ω) =

S_A (ω) = S_z(ω + ω_н)

S_a (ω) = S_A(ω - ω_н) + = S_A(ω + ω_н)

Комплексная огибающая радиосигнала A(t) является обобщенным параметром, который содержит полную информацию об амплитудной и угловой модуляции (полную информацию об управляющем колебании S(t)). Эту информацию и нужно сохранить при дискретизации радиосигнала.

A(t) – узкополосный сигнал, спектр которого сосредоточен в интервале частот от - Δ ω_a до + Δ ω_a, т.е. ω_в = Δ ω_а .

Тогда, в соответствии с теоремой Котельникова

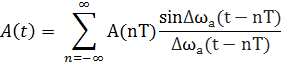
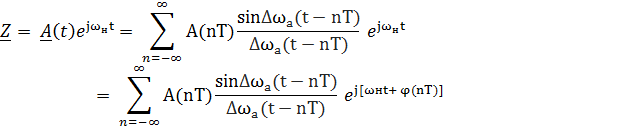
a (t) = Re Z (t) учитывая, что A (nT) = A(nT) e^jφ(t) , то получим

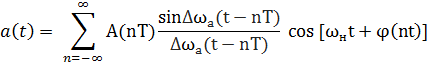
Как видим, при таком подходе временная дискретизация радиосигнала сводится к временной дискретизации огибающей и фазы радиосигнала, то есть радиосигнал полностью определяется отсчетами своей огибающей и своей фазы, взятых через интервал T ≤

В частном случае АМ:

a(t) = A(t)cos ω_нt

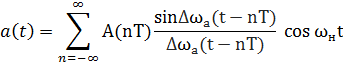
2 Δω_a = Ω_max ; ω_н = Ω_{max ;} T ≤

Для ЧМК:

a(t) = A₀ cos [ω_нt + φ(t)]

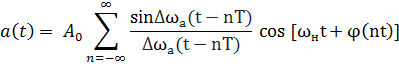
2 Δω_a = 2ω_дев(m>>1)

ω_дев – девиация частоты

ω_дев >> Ω_max ; ω_дев = m Ω_max

T ≤

В общем случае нужно осуществлять дискретизации комплексных отсчетов A(nT).

Для выхода из этой ситуации была предложена квадратурная дискретизация радиосигнала.

a (t) = A(t)cos [ω_нt + φ(t)]

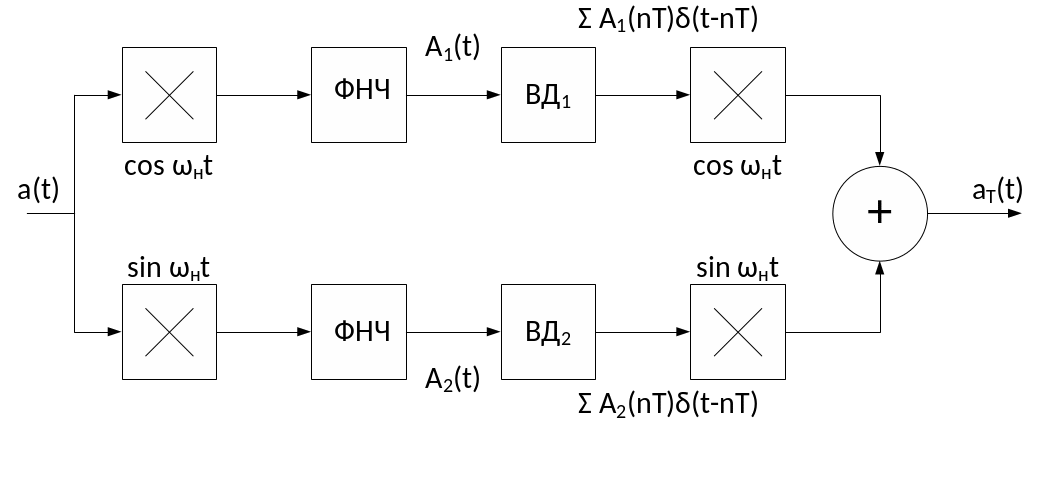
a (t) cos ω_нt = A(t) cos φ(t) + A(t) cos [2ω_нt + φ(t)]

a (t) sin ω_нt = - A(t) sin φ(t) + A(t) sin [2ω_нt + φ(t)]

A₁(t) = A(t) cos φ(t)

A₂(t) = - A(t) sin φ(t)

Вывод ВД₁:

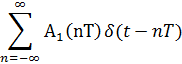
A₁ (nT) = A(nT) cos (nT)

Выход ВД₂:

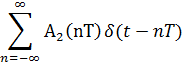
A₂ (nT) = - A(nT) sin φ (nT)

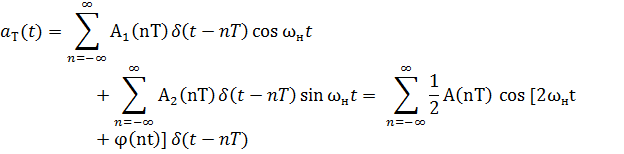
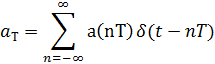
a(nT) = A(nT) cos [ω_нnT + ]