4.2 Синтез цифрового узкополосного фильтра низких частот на основе одноступенчатой децимации и интерполяции.

Пусть требуется синтезировать узкополосный КИХ – фильтр с заданными требованиями, и частотой избирательности.

Прежде всего, задаются параметры:

ω_с1 – частота среза полосы пропускания

ω_с2 – частота среза зоны непрозрачности

ω_д – частота дискретизации

α = показатель прямоугольности АЧХ фильтра (0.5…10)

β = показатель узкополосности АЧХ фильтра (10…10_­⁴)

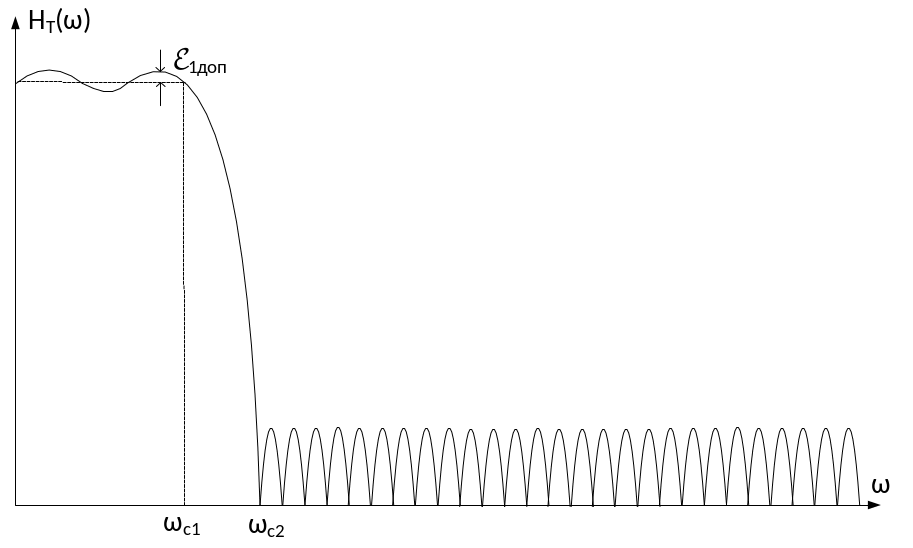
Допускается определенная неравномерность АЧХ в полосе пропускания

ε_1доп – допустимый уровень неравномерности

ε_2доп – допустимый уровень боковых лепестков в зоне непрозрачности

L(ε_1доп, ε_2доп) = - log(10 ℰ_1доп * ℰ_2доп) – логарифмический показатель частотной избирательности.

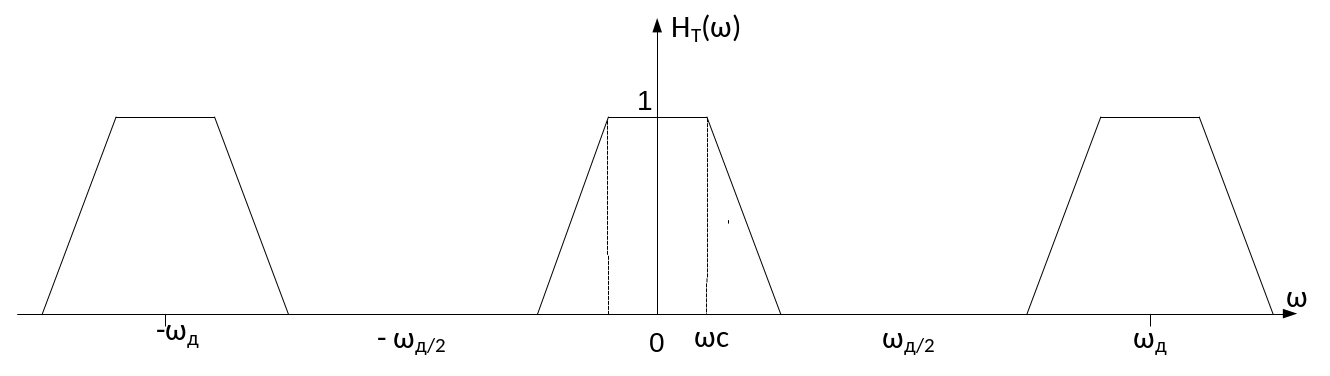
АЧХ КИФ – фильтра

ω_с1<< ω_д

Требуемый порядок нерекурсивного фильтра низких частот:

N = α*β* L(ε_1доп, ε_2доп)

Известно, что вычислительные затраты для получения отклика связаны с порядком фильтра.

В узкополосном фильтре определяющую роль играет β.

N ~ β, β ~ ω_д, при заданной ω_с1

Для уменьшения N, L, β нужно уменьшить частоту дискретизации (ω_д).

Децимация – способ снижения вычислительных затрат в ν раз.

ν =

Рассмотрим способ построения узкополосного КИХ – фильтра на основе одноступенчатой децимации и интерполяции.

В этой структуре дважды присутствует ФНЧ с заданными параметрами частотной избирательности (α, β, L) отсюда получается, что N*ω_д1 – исходная.

Как известно, в фильтре - дециматоре вычислительные затраты меньше в ν раз по сравнению с обычными и фильтрами.

Если ω_с1 < , то дециматор работает правильно.

В интерполяторе вычислительные затраты сокращаются в ν раз.

Выясним, получается ли выигрыш в вычислительных затратах при таком построении КИХ – фильтра.

В обычном КИХ – фильтре вычислительные затраты равны N, а при одноступенчатой децимации и интерполяции пропорционально . Выигрыш в вычислительных затратах

Найдем максимально возможный коэффициент децимации ν.

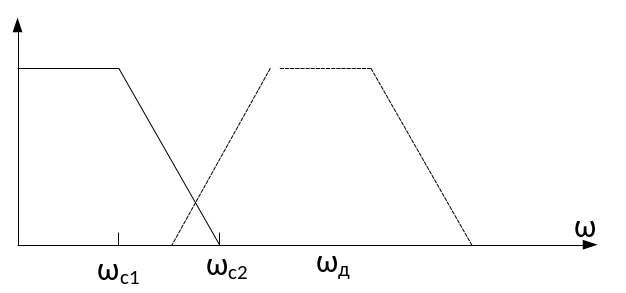
ν_max =

ω_д2min = ω_c2 + ω_c1 → ν_max =

ν = = = = = =

Если α >>1, тогда ν_max ≈ → N и ν увеличивается, выигрыша нет.

В тоже время сохраняется линейная зависимость вычислительных затрат от α. Для уменьшения вычислительных затрат было предложено перейти от одноступенчатой к многоступенчатой децимации и интерполяции.

4.3 Синтез цифрового узкополосного ких – фильтра на основе многоступенчатой децимации и интерполяции.

1. Метод Беланже

Метод Беланже заключается в каскадном включении предельно простых фильтров – дециматоров и фильтров – интерполяторов с коэффициентом децимации равным двум.

ν = 2^k → k = log₂ ν

Еще включают дополнительный ФНЧ, работающий на самой низкой частоте дискретизации, которая обеспечивает требуемую треугольность АЧХ (α = α₀)

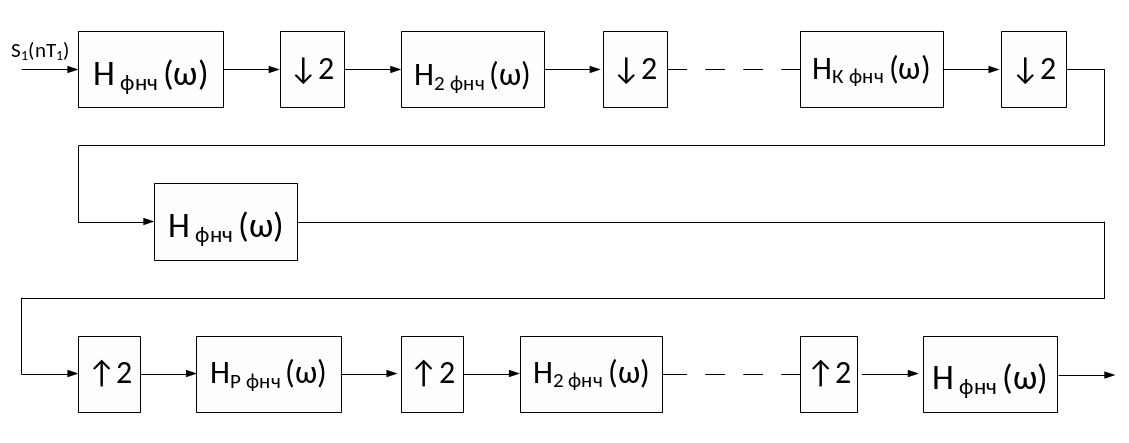
В этой схеме на ФНЧ₁, стоящий в первом дециматоре не накладываются высокие требования к прямоугольности А ЧХ, т.е

ФНЧ₁ – ω_д1, β₁=β, α₁<<α, т.к. ω_с1 →

ω_с2 » ω_с1 → α₁β = → 2 – минимально возможное значение

N₁ < N в раз

N₁ ≈ (N₁ << N)

ФНЧ₂ - ω_д2 = ; β₂ = ; α₂ = 2α₁

α₂ β₂ = α₁β

N₂ = N₁ << N

Тоже самое относится к другим фильтрам.

Исключение составляет ФНЧ₀

α₀ = α; ω_д0 =

N₀ =

Если пренебречь вычислительными затратами k – фильтров – дециматоров и интерполяторов , то оказывается, что вычислительные затраты этой структуры определяются формирующим фильтром, но они в ν раз меньше, чем в обычном фильтре без децимации. Однако, этот метод обладает недостатками:

1) недостаток связан с большим количеством фильтров – дециматоров и фильтров – интерполяторов. С ростом числа k растет ошибка ε_{1. ­}Для ее компенсации требуется повысить точность частотных характеристик фильтров, что увеличит их порядок.

2) ν должно быть кратно двум