3.4 Особенности синтеза бих - фильтра

Обычная или прямая форма построения БИХ фильтра.

Если разделить общий сумматор на 2 отдельных для рекурсивной и не рекурсивной части , то получаем два последовательно соединенных фильтра ( не рекурсивный, рекурсивный).

Поменяем местами 2 половинки

Как видим, в обе линии задержки подается один и тот же сигнал, поэтому они будут содержать одинаковые наборы отсчетов. Это позволяет объединить линии задержки.

КАНОНИЧЕСКАЯ ФОРМА БИХ-ФИЛЬТРА

При такой форме построения получается существенная экономия элементов ячеек памяти.

Однако, каноническая форма представления неудобна при большом порядке т.к.:

1. Абсолютные величины сигналов, проходящих через линии задержки могут существенно превосходить амплитуду входного и выходного сигнала, что потребует увеличение разрядности чисел в линии задержки, по сравнению с разрядностью входного и выходного сигнала, что усложняет реализацию.

2. С увеличением порядка фильтра m многократно увеличивается чувствительность частотных характеристик фильтра к неточному представлению коэффициента и , что может привести к потере устойчивости фильтра .

Поэтому на практике при большом порядке фильтра m применяют последовательную (каскадную) форму реализации БИХ фильтра в виде последовательного соединения звеньев 1 и 2 порядка.

Как известно, системная функция БИХ фильтра является дробно-рациональной, т.е . представляет собой отношение 2х полиномов.

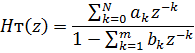
является дробно-рациональной, то есть представляет собой отношение двух полиномов.

Для реализации такого фильтра требуется выполнить два условия:

1)Физическая осуществимость – степень полинома в знаменателе должна быть больше или равна степени полинома в числителе N M

2) Устойчивость цепи – все полюсы функции (z) должны быть расположены на плоскости z внутри круга единичного радиуса с центром в начале координат, что соответствует левой полуплоскости комплексной переменной Р.

Ранее было показано, что для устойчивости линейной цепи все полюсы её передаточной функции Н(р) должна находиться в левой полуплоскости комплексной переменой Р.

Для примера рассмотрим БИХ фильтр второго порядка:

Перепишем в виде:

Нули знаменателя являются полюсами :

*Если – действительные полюсы,

* Если – комплексно - сопряженные полюсы.

Можно показать, что коэффициентs b1 и b2 связаны с полюсами следующим образом:

Раздел 4. Многоскоростная обработка сигналов при цифровой фильтрации.

1. Понятие вторичной частоты дискретизации цифровых сигналов. Децимация и интерполяция.

При цифровой обработке сигналов иногда возникает потребность в изменении частоты дискретизации обрабатываемого сигнала (обычно в целое число раз) либо в сторону уменьшения (децимация), либо в сторону увеличения (интерполяция).

1. Децимация (прореживание).

Децимация – это понижение частоты дискретизации в  раз.

При децимации речь идет о повторной(вторичной) дискретизации дискретного сигнала с частотой дискретизации или с интервалом дискретизации:

Будем считать, что этот сигнал получен путем временной дискретизации, в соответствии с теоремой Котельникова, аналогового сигнала с ограниченным спектром.

или

В принципе дискретизацию можно осуществить прореживанием исходной последовательности отсчётов.

Однако при повторной дискретизации нарушаются требования теоремы Котельникова, т.к. спектр дискретного сигнала является периодически повторяющимся и ограничен .

По теореме Котельникова:

На самом деле: в  раз.

Для выхода из этой ситуации перед вторичной дискретизацией нужно ограничить спектр исходного дискретного сигнала с помощью фильтра нижних частот.

В качестве такого фильтра удобно применить нерекурсивный цифровой фильтр, работающий на частоте дискретизации . Устройство, осуществляющее такую вторичную дискретизацию, называется фильтром – дециматором.

Структурная схема такого фильтра:

Входящий в неё блок понижения в  раз частоты дискретизации, называют компрессором.

Изобразим спектральные диаграммы для различных точек этой схемы:

Как видим, при прохождении сигнала через фильтр-дециматор, даже при использовании идеального фильтра нижних частот появляются частотные искажения или шумы децимации.

При использовании реального ФНЧ эти эффекты проявляются сильнее.

Заметим, что по сравнению с обычным нерекурсивным ФНЧ N-го порядка фильтр-дециматор, в состав которого входит такой фильтр, позволяет уменьшить вычислительные затраты для получения отклика, т.к. при децимации можно вычислять лишь каждый -ый отсчёт выходного сигнала. Следовательно потенциально возможно уменьшение вычислительных затрат в  раз. (Мы это используем позже.)

2. Интерполяция.

Интерполяция – повышение частоты дискретизации в  раз.

В принципе процесс интерполяции можно реализовать путём расстановки в промежутки между отсчётами дискретного сигнала, следующими с периодом , нулевых отсчётов с интервалом , с последующей фильтрацией идеальным цифровым фильтром НЧ с частотой дискретизации и граничной частотой .

В качестве такого ФНЧ используется нерекурсивный фильтр. Устройство, осуществляющее таким образом восстановление прежней частоты дискретизации сигнала, называют фильтром – интерполятором.

Его структурная схема:

Входящий в неё блок повышения в  раз частоты дискретизации, называют экспандером.

Покажем временные диаграммы в соответствующих точках схемы фильтра – интерполятора:

Заметим, что по сравнению с обычным нерекурсивным ФНЧ N-го порядка фильтр-интерполятор, в состав которого входит такой фильтр, позволяет уменьшить вычислительные затраты для получения отклика в  раз, т.к. на него поступает прореженная последовательность с нулевыми отсчётами, положение которых известно, и отклик на них искать не нужно. (Это пригодится позже.)