3.3 Синтез нерекурсивного цифрового фильтра с использованием окон (весовых функций)

Оконный метод удобен при синтезе по передаточной функции или АЧХ фильтра. Дело в том, что из – за периодического характера частотных характеристик ЦФ диапазон изменения цифровой частоты ограничен пределами:

где - частота дискретизации

Импульсная характеристика такого фильтра (t) как правило, является бесконечно протяженной, т.е. синтезируемый фильтр всегда получается рекурсивным.

Поясним это, воспользовавшись примером связи спектральных характеристик одиночного импульса и периодической последовательности таких импульсов.

Пусть S(t) прямоугольный импульс длительностью Тu, а период следования таких импульсов равен T. Два этих сигнала и соответствующие им спектральная характеристика S( ) и комплексные амплитуды Ск приведены на рисунке.

Так как основные соотношения, характеризующие преобразование Фурье, являются дуальными, то есть позволяют менять переменные местами, можно на нашем примере установить соотношение между импульсной характеристикой ЦФ и импульсной характеристикой его АФ прототипа.

Если синтезированный ЦФ является достаточно узкополосным ФНЧ с прямоугольной АЧХ и частотой среза , то его аналоговый фильтр прототип тоже узкополосный ФНЧ с прямоугольной АЧХ и частотой среза .

Если , то

Для получения КИХ фильтра необходимо усечь эту бесконечную последовательность , т.е. выбрать из нее центральный фрагмент конечной длины.

Такое простое усечение последовательности отсчетов импульсной характеристики соответствует использованию прямоугольного окна.

Однако в результате такого усечения происходит искажение первоначально заданной прямоугольной АЧХ (происходит свертка исходной АЧХ со спектром прямоугольного окна) .

ЧЕМ НОВАЯ АЧХ ОТЛИЧАЕТСЯ ОТ ИСХОДНОЙ?

1. Появляется переходная полоса между областью пропускания и областью задерживания.

2. Появляются колебания коэффициента усиления ( передачи) в полосе пропускания.

3. АЧХ в полосе задерживания, как правило, приобретает лепестковый характер.

На рисунке приведена типичная АЧХ (односторонняя ) КИХ – фильтра :

Заметим что степень этих искажений зависит от N( порядка фильтра) и частоты сре :

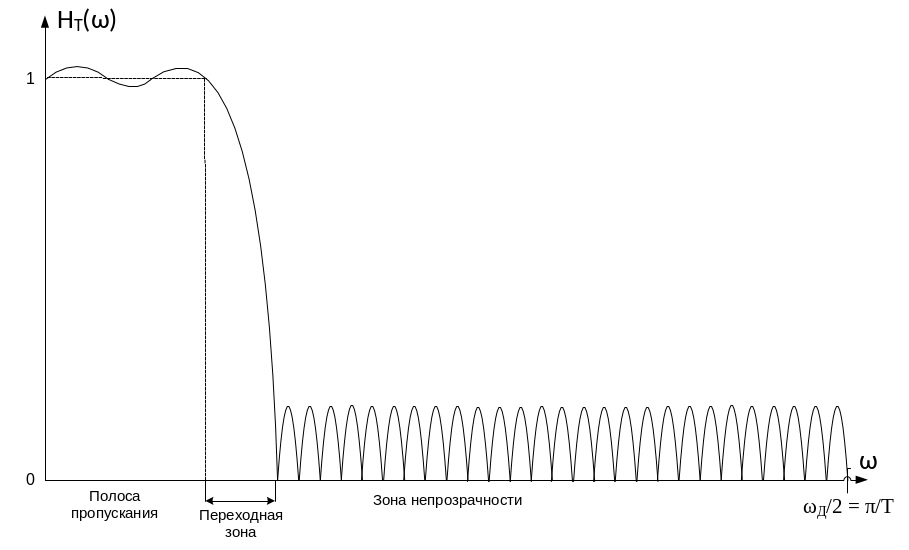
Рассмотрим пример ЦФ с прямоугольной АЧХ и частотой среза, равной

,

Импульсную характеристику ограничим пределами: -16≤ k ≤ 16

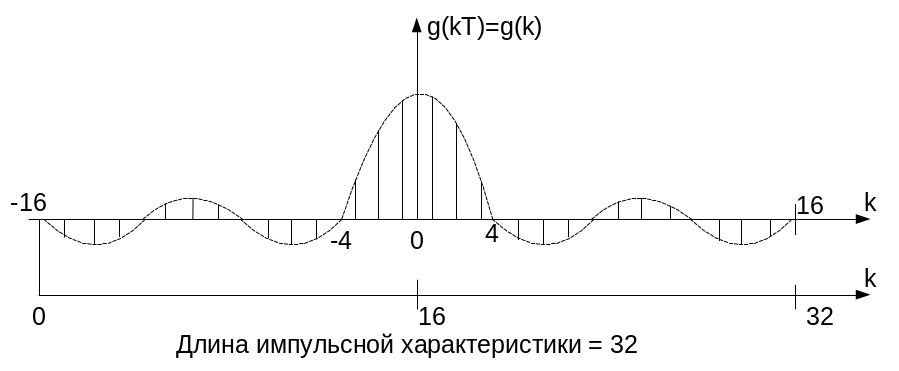
Физическая реализация такой импульсной характеристики невозможна , т.к отклик не должен появляться раньше воздействия . Поэтому в реальных не рекурсивных фильтрах импульсную характеристику задерживают на половину её длины.

Для ослабления этих искажений в первую очередь для уменьшения уровня боковых лепестков в полосе задерживания усеченную импульсную характеристику можно умножить на весовую функцию, плавно спадающую к краям , т.е. использовать не прямоугольное окно .

В литературе по «ЦОС» приводятся данные по уровню боковых лепестков в зоне задерживания для различных весовых функций (окон). Причем эти данные также зависят от порядка фильтра N и частоты среза.

НАПРИМЕР при N=256 , и = для прямоугольного окна уровень боковых лепестков в зоне задерживания равен – 21 дБ ;

для треугольного окна - 26.5 дБ;

для окна Ханна – 43.9 дБ;

для окна Хэмминга – 53.8 дБ ;

для окна Кайзера – 45.2 дБ;

для окна Чебышева – 51.1 дБ ;

Кроме уровня боковых лепестков, в зависимости от типа окна, меняется ширина переходной зоны, уровень пульсаций в ПП , а также показатели узкополосности и прямоугольности АЧХ.

Конкретные показатели для разных окон. Приводятся в известной литературе.